Side 1 av 1
Egenverdi og egenvektor
Lagt inn: 19/04-2017 13:02
av danode
Hei!
Har følgende matrise:
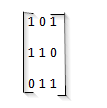
- matrise.png (1.53 kiB) Vist 2492 ganger
Ut i fra denne skal jeg finne egenverdier og egenvektorer til matrisen. Jeg kommer frem til egenverdiene λ1= 0, λ2= 1,5+0,8i, λ3=1,5 -0.8i.
For egenvektoren til λ1 kommer jeg frem til (-1,1-0), men for de to andre sliter jeg med å løse opp for "i". Er det noen som skjønner hvordan man løser ut for denne?
Re: Egenverdi og egenvektor
Lagt inn: 19/04-2017 14:40
av DennisChristensen
danode skrev:Hei!
Har følgende matrise:
matrise.png
Ut i fra denne skal jeg finne egenverdier og egenvektorer til matrisen. Jeg kommer frem til egenverdiene λ1= 0, λ2= 1,5+0,8i, λ3=1,5 -0.8i.
For egenvektoren til λ1 kommer jeg frem til (-1,1-0), men for de to andre sliter jeg med å løse opp for "i". Er det noen som skjønner hvordan man løser ut for denne?
Det karakteristiske polynomet er gitt ved $$\chi (x) = \left(1-x\right)^3 + 1 = 1 - 3x + 3x^2 - x^3 + 1 = 2 - 3x + 3x^2 - x^3.$$
Ved inspeksjon ser vi at $(x - 2) | \chi (x)$. Utfører vi polynomdivisjonen ser vi at $$\chi (x) = (2-x)(x^2 - x + 1) = (2-x)\left(x - e^{\frac{\pi}{3}i}\right)\left(x - e^{-\frac{\pi}{3}i}\right).$$ Dermed får du egenverdiene $$\lambda_1 = 2, \lambda_2 = e^{\frac{\pi}{3}i}, \lambda_3 = e^{-\frac{\pi}{3}i}.$$
Du kan nå løse likningene $$\begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 0 & 1 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \lambda_i \begin{pmatrix} x \\ y \\ z \end{pmatrix}$$ for $i = 1, 2, 3$ for å finne de korresponderende egenvektorene.
Re: Egenverdi og egenvektor
Lagt inn: 20/04-2017 14:59
av 123
Denne matrisen er vel ikke fra oppgave 1 oblig 2 mat1110 2017?

Re: Egenverdi og egenvektor
Lagt inn: 09/05-2017 22:18
av oppgitt student
DennisChristensen skrev:danode skrev:Hei!
Har følgende matrise:
matrise.png
Ut i fra denne skal jeg finne egenverdier og egenvektorer til matrisen. Jeg kommer frem til egenverdiene λ1= 0, λ2= 1,5+0,8i, λ3=1,5 -0.8i.
For egenvektoren til λ1 kommer jeg frem til (-1,1-0), men for de to andre sliter jeg med å løse opp for "i". Er det noen som skjønner hvordan man løser ut for denne?
Det karakteristiske polynomet er gitt ved $$\chi (x) = \left(1-x\right)^3 + 1 = 1 - 3x + 3x^2 - x^3 + 1 = 2 - 3x + 3x^2 - x^3.$$
Ved inspeksjon ser vi at $(x - 2) | \chi (x)$. Utfører vi polynomdivisjonen ser vi at $$\chi (x) = (2-x)(x^2 - x + 1) = (2-x)\left(x - e^{\frac{\pi}{3}i}\right)\left(x - e^{-\frac{\pi}{3}i}\right).$$ Dermed får du egenverdiene $$\lambda_1 = 2, \lambda_2 = e^{\frac{\pi}{3}i}, \lambda_3 = e^{-\frac{\pi}{3}i}.$$
Du kan nå løse likningene $$\begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 0 & 1 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \lambda_i \begin{pmatrix} x \\ y \\ z \end{pmatrix}$$ for $i = 1, 2, 3$ for å finne de korresponderende egenvektorene.
Hei! Hadde noen fantastiske mennesker der ute hatt mulighet til å hjelpe til med egenvektorene [tex]v_{2}[/tex] og [tex]v_{3}[/tex] som korresponderer for egenverdiene [tex]\lambda_2 = e^{\frac{\pi}{3}i}[/tex] og [tex]\lambda_3 = e^{-\frac{\pi}{3}i}[/tex], klarer fint å finne [tex]v_{1}[/tex], men når det kommer til de to siste så blir det bare kaos. :/