matematikk.net

mhm

Din løsning gir: [tex]15,15499889[/tex]
Den egentelige løsningen gir: [tex]15,15367058[/tex]

[tex]1,328313767 \cdot 10^{-3}[/tex] forskjell.

jaja, det var da nært! Men hva vis du har avrundet svarene dine litt etter litt, og har bare ikke avrundet det siste svaret? Det kan få feilen til å stemme

Mulig jeg misforstår her, men går du ikke utifra at utgangsvinkelen med bakken er den samme som vinkelen mellom det høyeste punktet, startpunktet og bakken er det samme når den faktisk er en del mindre? Eller har jeg lest innlegget ditt feil?

Karl_Erik skrev:Mulig jeg misforstår her, men går du ikke utifra at utgangsvinkelen med bakken er den samme som vinkelen mellom det høyeste punktet, startpunktet og bakken er det samme når den faktisk er en del mindre? Eller har jeg lest innlegget ditt feil?

Jeg sa at det var en feil , det er altså den nøyaktigheten på selve svaret jeg lurte på hvorfor skjer(altså at svaret blir 15,15m)

mathme skrev:

Thales skrev:Forresten, jeg fant ut at:

[tex]max_{hoeyde}=\frac{tan(25)\cdot\frac{130}{2}}{2}=\frac{tan(25)\cdot{65}}{2}[/tex]

Noen som klarer å forklare hvorfor?

Hvordan kom du fram til det ?

Kan faktisk bevise det nå

Thales skrev:

mathme skrev:

Thales skrev:Forresten, jeg fant ut at:

[tex]max_{hoeyde}=\frac{tan(25)\cdot\frac{130}{2}}{2}=\frac{tan(25)\cdot{65}}{2}[/tex]

Noen som klarer å forklare hvorfor?

Hvordan kom du fram til det ?

Kan faktisk bevise det nå

Nehei ? Hadde vært utrolig kult!

ups tokk litt feil, beviset går litt ut på noe annet men poster det selv om det

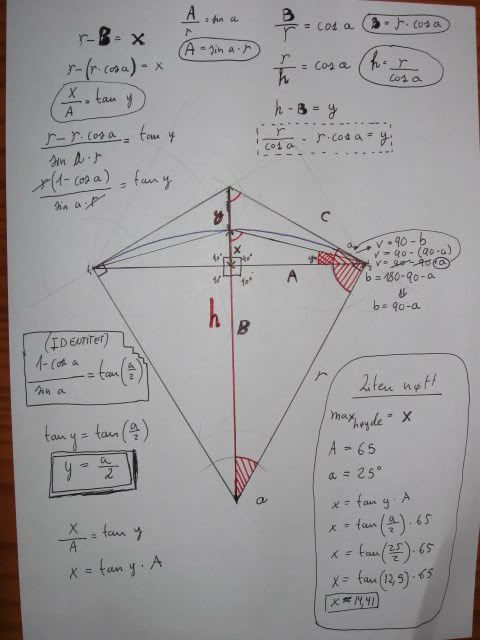
Kommer til det svaret hvor max høyde er [tex]\approx 14,41[/tex] men kanskje det er noe som jeg har oversett? i så fall vis dere finner noen feil bare si i fra. Vis dere ikke tror at identiteten stemmer sjekk(ikke noe å pirke på nå mathme ) den siste identiten på denne siden.

Oppfølger:

Hvis baseballspilleren skyter ballen med en vinkel [tex]\theta[/tex] på den skrå bakken som har vinkelen [tex]\phi[/tex] med horisontalplanet, hvor stor må starthastigheten være om han ønsker å skyte den bort med lengden [tex]L[/tex] langs skråplanet?
Vinklene er slik at summen av dem er mindre enn 90 grader.

Hva er maksimalhøyden på ballen?

Mulig jeg misforstår noe her, Thales, men antar du i beviset at ballen følger en sirkelbane? Det er nemlig ikke korrekt, den følger en parabel.

Bogfjellmo skrev:Mulig jeg misforstår noe her, Thales, men antar du i beviset at ballen følger en sirkelbane? Det er nemlig ikke korrekt, den følger en parabel.

I dette tilfellet er parabelen er en del av en sirkel ikke sant?

Thales skrev:
I dette tilfellet er parabelen er en del av en sirkel ikke sant?

Hva skal dette bety? En parabel og en sirkel har ikke samme form.

Parabler og sirkler er dog beslektet, og dette vil du finne ut mer om når du lærer om kjeglesnitt, Thales I fysikkens verden er det sjelden du finner helt sirkulære baner, (med unntak av ladede partikler som beveger seg i magnetfelt og systemer der bevegelsen er begrenset av et sirkulært spor.)

Jarle10 skrev:Oppfølger:

Hvis baseballspilleren skyter ballen med en vinkel [tex]\theta[/tex] på den skrå bakken som har vinkelen [tex]\phi[/tex] med horisontalplanet, hvor stor må starthastigheten være om han ønsker å skyte den bort med lengden [tex]L[/tex] langs skråplanet?
Vinklene er slik at summen av dem er mindre enn 90 grader.
Hva er maksimalhøyden på ballen?

Vi legger kastet inn i et koordinatsystem; y-aksen loddrett oppover og x-aksen bortover langs horisontalplanet. En vektorfunksjon som gir posisjonsvektoren til ballen er

[tex]\vec{r}(t)=[v_0 \cdot cos(\phi+\theta)t, v_0 \cdot sin(\phi+\theta)t-\frac{1}{2}gt^2][/tex]

I tillegg til origo vet vi at punktet [tex](Lcos\phi, Lsin\phi)[/tex] ligger på parabelen ballen følger. Det gir oss et par ligninger:

[tex]v_0 \cdot cos(\phi+\theta)t=Lcos\phi[/tex]

[tex] v_0 \cdot sin(\phi+\theta)t-\frac{1}{2}gt^2=Lsin\phi[/tex]

Vi finner et uttrykk for t av den første ligningen og setter dette inn for t i den andre ligningen. Jeg ender opp med dette uttrykket.

[tex]v_0=\left(\frac{Lgcos^2(\phi)}{2 \left(tan(\phi+\theta) cos(\phi)-sin(\phi) \right)cos^2(\phi+\theta)}\right)^{\frac{1}{2}}[/tex]



For å finne maksimalhøyde, deriverer vi y-komponenten av funksjonen og setter lik 0, og får ligningen

[tex]v_0sin(\phi+\theta)-gt=0[/tex]

[tex]t=\frac{v_0sin(\phi+\theta)}{g}[/tex]

Vi setter inn for t i y-komponenten av [tex]\vec{r}(t)[/tex] og ender opp med

[tex]y_{maks}=\frac{v_0^2sin^2(\phi+\theta)}{2g}[/tex]

Edit: kom på en mer elegant måte å finne [tex]y_{maks}[/tex]

I y-retning har vi at [tex](v_0 \cdot sin(\phi+\theta))^2=0+2gy_{maks}[/tex], og svaret følger direkte.