1P 2012 høst LØSNING
DEL EN
Oppgave 1
Butikk A : $ 2 \cdot 50kr =100kr. \quad$ I butikk A koster druene 100 kroner. (Du betaler for to beger = en kg, og får siste beger "gratis").
Butikk B: $1,5 \cdot 70kr = 105kr. \quad$ I butikk B koster druene 105 kr. Butikk A er billigst.
Oppgave 2
En vare som kostet 50 kr. koster nå 90 kr. Økningen er på 40 kr. Økningen i prosent er:
$ \frac{40 kr}{50 kr} = \frac{4}{5} = 0,80 = 80$%
Oppgave 3
a)
| Antall elever | 5 | 10 | 30 |
|---|---|---|---|
| Pris per elev (kr.) | 600 kr | 300 kr | 100 kr |
b)
Det koster $ 5 \cdot 600kr = 3000kr \quad $ å leie hytta.
Oppgave 4
$ 20L = 20 dm^3 = 0,020 m^3 $
4,4h = 4 timer og $0,4 \cdot 60$ min = 4 timer og 24 minutter
200 m/s = 200 m/s $\cdot$ 3600 s = 720 000 m/time = 720 km/h
Oppgave 5
$ \frac{2}{40} = \frac{5}{100} = 5$%
En ökning på 2 prosentpoeng, fra 40% til 42%, tilsvarer en økning på 5%.
Oppgave 6
I basisåret er indeksen 100. For å ha samme kjøpekraft må lønnsutviklingen følge indeksen:
$\frac{500000kr}{100} = \frac{x}{120} \\ 100x = 60000000kr \\ x= 600000kr$
Hun må tjene 600 000 kr for å ha samme kjøpekraft.
Oppgave 7
a)
| Int. Eng | Ikke Int. Eng. | TOTAL | |
|---|---|---|---|
| Sos. kun. | 5 | 9 | 14 |
| Ikke Sos. kun. | 7 | 4 | 11 |
| TOTAL | 12 | 13 | 25 |
b)
5 har valgt begge deler. Av 25 elever blir det: $ \frac{5}{25} = \frac 15 $
c)
Vi vet at eleven har valgt sos.kun. Av disse 14 har 5 valgt int. eng. Vi får: $ \frac{5}{14}$
Oppgave 8
Ett Pund er 4 Litas. Fire Litas ganges med 2,25 og gir 9 NOK (Norske kroner). Ett pund tilsvarer altså 9 NOK.
Oppgave 9
Trekanten er likebeint.
a)
$\angle B = 48,2^{\circ} \\ \angle C = 180^{\circ} - 48,2^{\circ} -48,2^{\circ} = 83,6^{\circ}$
Påstanden i a er riktig.
b)
Vi er på del en og har ikke kalkulator. Høyden fra C på linjestykket AB finner vi ved å bruke Pytagoras:
Høyde: $\sqrt{6^2-4^2} = \sqrt{20} $
Areal trekant: $A= \frac{g \cdot h}{2} = 4 \cdot \sqrt{20}$
Dersom arealet skal bli 20 må høyden være lik 5. Kvadratroten av 20 er mindre enn 5 siden kvadratroten av 25 er 5. Arealet av trekanten er derfor mindre enn 20 og påstanden er sann.
Oppgave 10
a)
b)
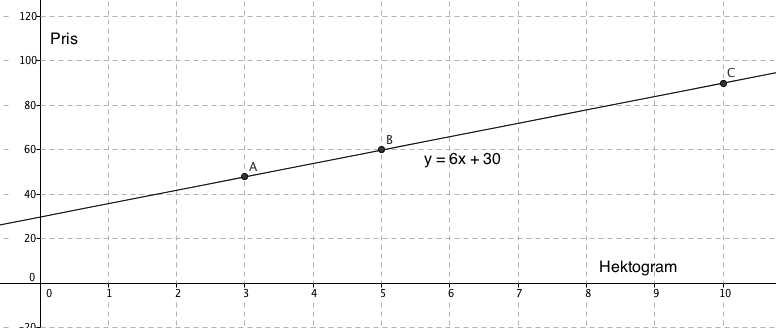
Det ser ut som om grafen krysser y aksen i 30, dvs. et tomt påskeegg koster 30 kr. Fra 0 til 10 hektogram stiger prisen med 60 kroner. Det betyr at et hektogram koster 6 kroner. Funksjonsutrykket blir: y = 6x + 30, der x er antall hektogram, og y er prisen man betaler.
c)
Setter y = 81 i likningen i b, og løser den:
$ y=6x+30 \\ 81 = 6x + 30 \\ 6x = 51 \\ x = \frac{51}{6} \\ x= 8,5$
Man får 8,5 hektogram smågodt for 81 kroner.
DEL TO
Oppgave 1
Ordinær lønn: $90kr \cdot 150 = 13500 kr$
Overtid: $ 90kr \cdot 1,6 \cdot 10 = 1440 kr$
Lønn : 14940 kr.
Skatt:$14940 kr \cdot 0,18 =2689,20kr$
Han betaler 2689,20 kr i skatt.
Oppgave 2
$12000kr \cdot 1,045^{15} = 23223,40kr$
Etter femten år står det 23.223,40 kr på kontoen.
Oppgave 3
a)
Arealet av grunnflaten er: $grunnflate = 14m \cdot 7 m + 1m \cdot 4m =102 m^2$
Arealet av sålen, det lyseblå arealet er $13,5m \cdot 6,5m + 1m \cdot 3,5m = 91,25 m^2$
Areale av grunnmur er areal av grunnflate minus areal av såle: $Grunnmur = 102m^2 . 91,25 m^2 = 10,75m^2$
b)
Volum. $91,25m^2 \cdot 0,1m + 10,75m^2 \cdot 0,4m = 13,425 m^3$
Han trenger 13,4 kubikkmeter betong.
Oppgave 4
a)
$\frac{I_{2010}}{I_{1989}} = \frac{177,2}{68,6} = 2,59$
En vekstfaktor på 2,59 tilsvarer 159% økning.
b)
Indeksen øker med 39,7% i perioden. Dersom boligen følger indeksen blir verdien i 2006: $1700000 \cdot 1,397 = 2374900$
Verdien er ca 2 375 000 i 2006,
c)
Dersom boligen følger indeksen blir verdien i 2010: $1700000 \cdot 1,772 = 3012400$
Prisen de betalte for boligen i 2000 tilsvarer ca 3 mil. i 2010 kroner. Gevinsten er derfor ca. 400.000 kr.
Oppgave 5
| Pizza | Pølse | TOTAL | |
|---|---|---|---|
| Salat | $0,75 \cdot 0,5 = 0,375$ | $0,25 \cdot 0,2 = 0,05$ | 0,425 |
| Ikke Salat | $0,75 \cdot 0,5 = 0,375$ | 0,20 | 0,575 |
| TOTAL | 0,75 | 0,25 | 1 |
a)
Sannsynlighet for pølse men ikke salat er ut fra krysstabellen 20%
b)
42,5% vil ha salat. Av 200 elever blir det 85 elever.
Sannsynligheten for at en elev vil ha salat er 42,5%
Oppgave 6
a)
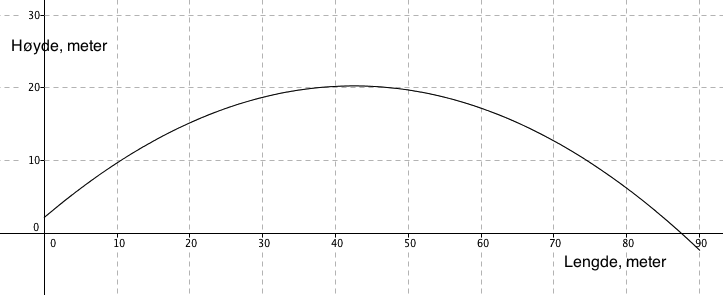
Figuren viser grafen til $f(x) = -0,01x^2 + 0,85x +2,2$ i intervallet 0 til 90.
b)
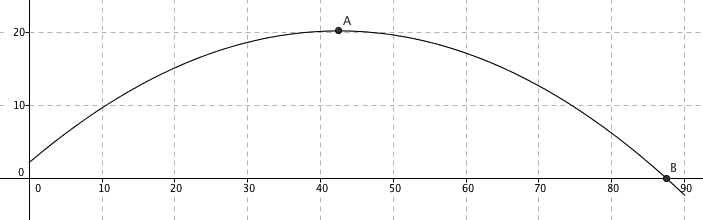
Bruker digitalt verktøy og finner at toppunktet A er ( 42,5 , 20,26 ) og nullpunktet B er ( 87,51 , 0 )
c)
Skjæring med y aksen er 2,20 meter. Det betyr at når spydet forlater kasterens hånd har det en høyde på 2,20 meter. Den maksimale høyden når spydet når det har beveget seg 42,5 meter bortover. Høyden er da 22,26 meter over bakken. Kastet er 87,51 meter langt.
Oppgave 7
a)
Bruker Pytagoras og finner høyden:
$h = \sqrt{6^2 - 4,5^2} =4,0$
Høyden i glasset er 4,0 cm.
b)
Volum av kjeglegormet glass:
$V = \frac 13 \pi r^2h = \frac 13 \pi \cdot 4,5^2 \cdot 4,0 cm^3 = 84,2 cm^3$
Glasset rommer altså $84cm^3$ som er det samme som 84, 2 ml eller 8,4 cl eller 0,84 dl.
Oppgave 8
a)
Per reiser 300km med en gjennomsnittsfart på 60km/time. 300km : 60 km/time = 5 timer. Siden han startet kl 10.00 er han framme kl 15.00.
Kari skal reise samme strekning. Hun starter 10.30 og sitter to timer på bussen. Hun går på toget 12.45. Toget har en snittfart på 100km/time, og hun skal 200 km med tog, altså to timer på toget. Hun er da framme 14.45, 15 minutter før Per.
b)
Per har kjørt i to timer og 45 minutter når Kari går på toget, altså 2,75 timer. Med en snittfart på 60 km/time blir det 165 km.
Om vi ser på situasjonen etter 12:45 er Per tilbakelagte distanse gitt ved P = 165 + 60t og Karis tilbakelagte distanse med K = 100 + 100t. Setter P=K.
$P=K \\ 165 + 60t = 100+ 100t \\ 40t =65 \\ t= 1,625$
Dette er 1,625 timer etter 12:45, altså 1 time og 0,625 *60 minutter = 37, 5 minutter. De passerer hverandre kl. 14:22:30
c)
Dersom de skal komme fram sammtidig må Per gasse på. Han må bruke 4,75 timer på 300 km.
$\frac {300km}{4,75} = 63,2 km/t $
Han må holde en snittfart på ca. 63,2 km/time, om de skal komme fram sammtidig.