1P 2014 høst LØSNING
- Diskusjon av denne oppgaven
- Alternativ løsning fra mattepratbruker kongsberg (ikke kvalitetssikret av matematikk.net
- Alternativt løsningsforslag fra NDLA
DEL EN
Oppgave 1
Økningen i tallverdi er den samme hvert år, 1000 bøker. Den prosentvise økningen blir da størst når grunnlaget er minst, altså fra 2010 til 2011. Da er grunnlaget 4000 bøker og den prosentvise økningen er på 25%.
Oppgave 2
Til ni personer trenger man x gram kjøttdeig:
$\frac {500}{4} = \frac{x}{9} \\ x= \frac{500 \cdot 9}{4} \\ x = 1125$
Man trenger 1,125 kilogram kjøttdeig til ni personer.
Oppgave 3
I et basisår er indeksen 100. I 2013 er indeksen for varen lik x.
$\frac{600}{100} = \frac{720}{x} \\ x= \frac{720 \cdot 100}{600} \\ x= 120 $
I 2013 var indeksen for varen 120, altså en økning på 20% fra basisåret.
Oppgave 4
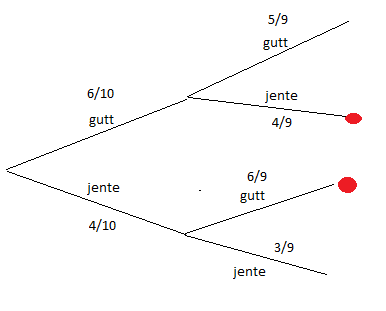
Det er to muligheter, gutt - jente og jente - gutt:
$P(en \quad av \quad hver) = \frac{6}{10} \cdot \frac{4}{9} + \frac{4}{10} \cdot \frac{6}{9} = \frac{8}{15} $
Oppgave 5
Dersom to størrelser, x og y er proporsjonale er:
y = kx
der k er proporsjonalitetskonstanten.
Trond mener det er proporsjonalitet og kan argumentere med følgende:
Dersom du betaler 10 kroner for 4 kiwi koster en kiwi 2,50 kroner. Om du kjøper 8 kiwi og betaler 20 kroner koster en kiwi fortsatt 2,50 kroner. Trond kan da sette opp følgende:
Totalpris for x antan kiwi = 2,50 koner ganger x antall kiwi,
og derved argumentere for proporsjonalitet.
Therese mener det ikke er grunnlag for å hevde proporsjonalitet. Hun kan argumentere som følger:
Hva om man kjøper en kiwi? Det står ingenting om at en kiwi koster kr. 2,50. Hva om man ønsker å kjøpe 100 kiwi? Det kan tenkes at vi kan presse prisen under kr. 250, det vet vi ingen ting om.
Ut fra foreliggendeinformasjon er det ikke grunnlag for å hevde hverken det ene eller det andre.
Oppgave 6
a)
Det betyr at prisen øker med samme beløp hvert år.
b)
En lineær funksjon er på formen y = ax + b:
Varen har steget med 50 kr. hvert år fra å koste kr. 600 i 2006, til 1000kr i 2014.
f(x) = 50x + 600
c)
2018 er 12 år etter 2006:
$f(12) = 50 \cdot 12 + 600 = 1200$
I 2018 vil varen koste 1200 kroner, om prisutviklingen fortsetter som før.
Oppgave 7
a)
Før lunch: Det var fem ganger så mange barn ute som inn, derfor er det x barn inn og 5x barn ute.
Etter lunch: Tre barn som var inne gikk ut. Derfor er det nå (x- 3) barn inne og (5x + 3) ute.
Etter lunch er det åtte ganger så mange barn ute, som inne. Det gir
8(x - 3) = 5x + 3
b)
$8(x-3)= 5x+3\\ 8x-24=5x+3 \\ 8x-5x = 24+3 \\ 3x = 27 \\ x=9$
Før lunch var det 9 barn inn og $5 \cdot 9$ barn ute. Det var altså 9 + 45 = 54 barn i barnehagen den dagen.
Oppgave 8
a)
Det man betaler tilbake til banken er et terminbeløp. Terminbeløpet er summen av renter og avdrag.
Et annuitetslån har et konstant terminbeløp. Det betyr at man betaler mest renter i begynnelsen og gradvis større avdrag, når renteinnbetalinger. Et annuitetslån er totalt sett dyrere enn et like stort serielån.
b)
Solveig tar opp et serielån, samme rentesats og samme løpetid på lånet, som Sivs annuitetslån. Serielån er da normalt totalt sett billigere enn annuitetslån, men man betaler mere i starten.
c)
Fordelen med et annuitetslån i forhold til serielån er at man betaler banken et mindre beløp hver måned, enn med serielån, i STARTFASEN. Det er jo ofte da man har dårligst råd. Denne fordelen betaler man imidlertid for, da totalbeløpet som tilbakebetales ved annuitetslån er større enn for tilsvarende serielån.
Oppgave 9
a)
Bruker Pytagoras:
$(PQ)^2 = 12^2 + 5^2 = 144 + 25 = 169 \\ PQ = \sqrt {169} = 13$
( Fordi 13 ganger 13 er 169)
b)
Figur 1: $O= 11+11 + 5,5 \pi = 22 +5,5 \pi $
Figur 2: $O= 13 + 2,5\pi + 6,0\pi = 13 + 8,5\pi $
$22-13 =9 \\ 8,5\pi - 5,5 \pi = 3 \pi \\ 3 \pi > 9$
Figur to har størst omkrets.
DEL TO
Oppgave 1
a)
Det er 3600 sekunder i en time:
$45 \cdot 3600 = 162000$
162.000 personer hadde logget seg på i løpet av en time.
b)
$900000 : 162000 = 5,55$
Det vil ta ca. fem og en halv time. 5,55 timer = 5 timer $+ 0,55 \cdot 60$ minutter, altså fem timer og trettitre minutter.
c)
900000 + 3,7 mill = 4,7 mill.
$\frac{0,9mill \cdot 100%}{4,6} = 19,6%$
Ca 19,6% er elektroniske brukere.
Oppgave 2
a)
b)
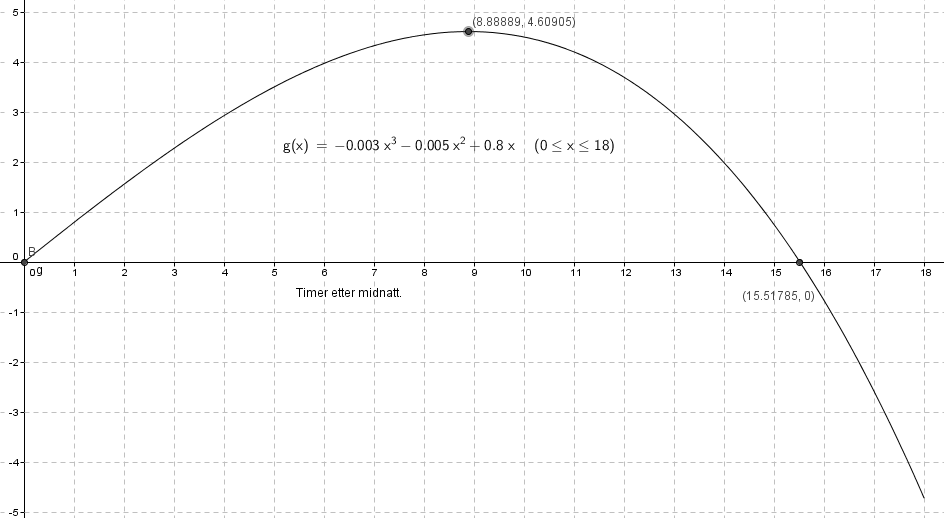
Leser av grafen i a og finner at nullpunkter er (0,0) og (15,52 , 0).
Toppunktet er (8,89, 4,61), fra grafen i a.
c)
Snøen begynte å legge seg ved midnatt. Den nådde et maksimum på 4,6 cm. etter ca. ni timer, altså rett før ni på morgenen. Snøen smelter raskt utover ettermiddagen og er borte ca. halv fire.
Oppgave 3
a)
b)
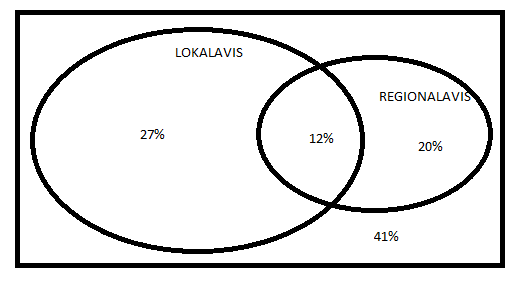
P (Lokalavis gitt regionalavis) = P(L|R) $= \frac{12}{32} = 0,375 = 37,5$%
Det er 37,5% sjanse for at man holder lokalavisen, dersom man holder regionalavisen.
c)
Her teller bare lokalavisen. 39% holder den. 61% holder den ikke.
P( av tre utvalgte finnes bare en abonnent.) = $0,39 \cdot 0.61 \cdot 0,61 + 0,61 \cdot 0,39 \cdot 0,61 + 0,61 \cdot 0,61 \cdot 0,39 = 0,435 = 43,5$%
Det er 43,4 prosent sjanse for at kun en av tre utvalgte er abonnent.
Oppgave 4
a)
$\frac{DE}{2,4cm} = \frac {20cm}{4cm} \\ 4DE = 48cm \\ DE = 12 cm$
b)
Forholdet mellom $\triangle$ ABC og $\triangle$ BDE er 1:5.
BC + BD = BC + 5BC = 6BC = 16,8cm
BC = 2,8 cm.
c)
Areal trekant ABC: $A= \frac{g_{ABC} \cdot h_{ABC}}{2} = 3,3cm^2$
Areal trekant BDE: $A= \frac{5g_{ABC} \cdot 5h_{ABC}}{2} = 25 \cdot 3,3cm^2 = 82,5cm^2$
Oppgave 5
a)
Volum sopp = volum halvkule + volum sylinder:
$V= \frac12 \cdot \frac 43 \pi (4dm)^3 + \pi \cdot (2dm)^2 \cdot 4dm \\ V = 134,04 dm^3 + 50,27 dm^3 = 184,31 dm^3 $
b)
Vi maler ikke sylinderens underside.
Radius sylinder = r
Radius halvkule = R
Overflate av sopp minus grunnflate i sylinder:
$O = 2\pi \cdot r \cdot R + \frac12 \cdot 4 \pi R^2 + (\pi R^2 - \pi r^2) \\ O = 2 \pi \cdot 2dm \cdot 4dm + 2 \pi (4dm)^2 + \pi ((4dm)^2- (2dm)^2) \\ O = 188,5 dm^2 $
Maling: $1,885m^2 : 6 m^2/l = 0,31 liter$
Oppgave 6
a)
Husk at justeringen er etterskuddsvis i Januar, altså i forhold til indeksen året før.
$\frac{8000 kr}{128,8} = \frac{x}{130,4} \\ x= \frac{8000kr \cdot 130,4}{128,8} \\ x= 8099,38 \approx 8100 kr. $
b)
Leien for 2013 blir justert i januar 13, i forhold til indeksen for 2012.
Leie 2012 + leie 2013 = $8100kr \cdot 12 + \frac{8100kr \cdot 131,4}{130,4} \cdot 12 \\ 97200 kr + 97956 kr = 195156kr.$
Oppgave 7
a)
$75000 \cdot 1,0175^3 = 79006,81kr.$
Han har 79006,81 kroner på konto i januar 2017.
b)
$((25000kr \cdot 1,045 + 25000kr) \cdot 1,045 + 25000kr) \cdot 1,045 = 81954,78 kr $
c)
I løpet av denne tiden setter han inn 75000 kroner. 20% av 75000kr er $75000kr \cdot 0,2 = 15000kr$. Dette er beløpet han får i skattelette i løpet av perioden.
d)
Arne "tjente" 4006,81 kroner i renteinntekter.
Eirik "tjener" 6954,78 kroner i renteinntekter. I tillegg sparer han 15000 kroner på skatten. Det blir tilsammen 21954,78 kroner.
$\frac{21954,78}{4006,81} - 1,0 = 4,4794$
som tilsvarer ca. 448%.
Oppgave 8
Fra grafen ser man at dersom Jensen bruker 28 timer på jobben er timelønnen kr. 1000,- Det betyr at han får 28000 kroner for å male huset.
28000 kr. : 64 timer = 437,50 kr/ time.
Han tjener 437,50 kroner per time, dersom han bruker 64 timer på malerjobben.