1T 2011 høst LØSNING
DEL EN
Oppgave 1:
a)
<math> \frac{x^2-25}{x^2+10x+25} = \frac{(x+5)(x-5)}{(x+5)(x+5)} = \frac{x-5}{x+5}</math>
b)
<math> 3^{2x-1} = 1 \\ 3^{2x-1} = 3^0 \\ 2x-1 = 0 \\ x= \frac 12</math>
c)
<math> \frac{a^{\frac 14} \sqrt a}{(a^{\frac 34})^3 \cdot a^{-2}}= a^{\frac 14 + \frac 24 - \frac 94 + \frac 84} = a^{\frac 12} = \sqrt a </math>
d)
<math> A= \frac {gh}{2} \\6= \frac {5h}{2} \\ h = \frac {12}{5} </math>
e)
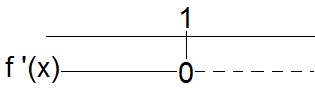
Ser fra figuren at:
<math> f(x) \leq 0 \quad \quad \quad x \in [1,3] \\ f(x) > g(x) \quad \quad x \in <\leftarrow,0>\cup <5, \rightarrow> </math>
f)
<math>tanC =2 \\ 2= \frac{AB}{AC} \\ AC = 1,5 </math>
g)
3 Blå, 2 røde, 1 grønn. Totalen er 6.
1) <math> \frac 56 \cdot \frac 45 = \frac 23 </math>
2) <math> \frac 36 \cdot \frac 25 + \frac 26 \cdot \frac 35 = \frac 25 </math>
h)
<math> f(x)=x^2+1 \\ \lim_{\Delta x\to 0}\quad\frac{f(x+ \Delta x) - f(x)}{\Delta x} = \\ \lim_{\Delta x \to 0}\quad\frac{(x+ \Delta x)^2 +1 - (x^2+1)}{\Delta x} = \\ \lim_{\Delta x \to 0}\quad\frac{x^2+2x \Delta x +( \Delta x)^2+1-x^2-1 }{\Delta x} = \\ \lim_{\Delta x \to 0}\quad\frac{2x \Delta x +( \Delta x)^2}{\Delta x} = \\ \lim_{\Delta x \to0}\quad\frac{\Delta x(2x + \Delta x)}{\Delta x} = \\ \lim_{\Delta x \to 0} \quad 2x + \Delta x = 2x</math>
Oppgave 2
a)
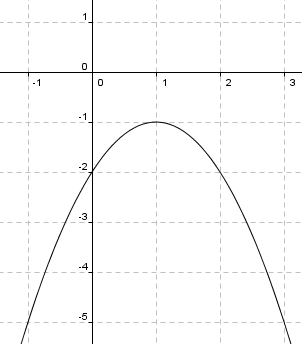
<math>f(x) = -x^2+2x-2</math>
Desom ingen nullpunkter må
<math>b^2-4ac <0 \\ 2^2-4 \cdot(-1) \cdot (-2) =-4</math>
Dvs. ingen nullpunkter
b)
<math>f'(x) = -2x+2 \\ f'(x)=0 \\ -2x+2 =0 \\ x=1</math>
Ekstremalpunkt: f(1) = -1, dvs. man har et maksimum i punktet (1,-1).
c)
f har en tangent i (2,-2)
Stigningstall: f'(2)= -2
y=-2x+b
-2 = -4 + b
b=2
Likning for tangent: y = -2x +2
Oppgave 3
a)
Tilnærmet: F = 2C + 30
Eksakt: 5F = 9C + 160
100 grader celsius er tilnærmet F = 230, altså 230 Farenheit. Eksakt er det:
<math> 5F = 9C +160 \\ 5F = 900 + 160 \\ F= 212</math>
Man observerer at forskjellen er 18 grader og at den tilnærmede metoden viser for mye ved 100 grader celsius.
b)
<math> \left[F=2C+30 \\ 5F = 9C +160 \right] \\ \left[F=2C+30 \\ 5(2C+30) = 9C +160 \right] \\C = 10 \wedge F = 50</math>
Det betyr at tilnærmingen er helt riktig når temperaturen er 10C (50F), men at den blir mer og mer unøyaktig når temperaturen fjerner seg fra 10 grader celsius.
DEL TO
Oppgave 4.
a)
Dersom trekanten er rettvinklet må siden på 6cm være hypotenus.
<math>(6cm)^2 \neq (4cm)^2 + (5cm)^2 \\ 36cm^2 \neq 41cm^2 </math>
Trekanten er ikke rettvinklet.
b)
a = 4,0 cm
b = 5,0 cm
c = 6,0 cm
<math> a^2 = b^2 + c^2 - 2bcCosA \\ Cos A = \frac{16-25-36}{-2 \cdot 5 \cdot 6} = 0,75 \\ A = 41,4 ^{\circ}\\ Areal: \quad A = \frac 12 bcSinA = \frac 12 \cdot 5 \cdot 6 sin 41,4^{\circ} \\ A= 9,9cm^2 </math>
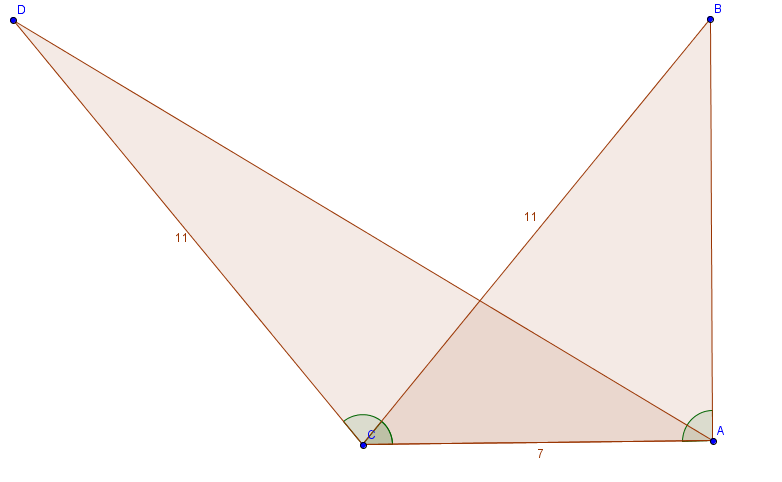
c)
<math> A= \frac 12 abSinC </math>
sinC har et maksimum for c = 90 grader, dvs. sinC=1.
<math> A= \frac 12 \cdot 11,0 \cdot 7,0 cm^2 = 38,5cm^2 </math>
d)
<math>A = \frac 12 absinC \\ 30cm^2 = \frac 12 \cdot 7cm \cdot 11 cm sinC \\ C =51,2^{\circ} \vee C= 180^{\circ} - 51,2^{\circ} = 128,8^{\circ}</math>
Oppgave 5.
a)
<math> V= \pi r^2h \\x=r \\d+h = 6 \\ h =6-2x \\V(x) = \pi x^2(6-2x) \\V(x)=6\pi x^2-2\pi x^3</math>
Man observerer fra h = 6 - 2x og fra x = r at <math>x \in <0,3> </math>
b)
<math>V'(x)= 12 \pi x -6 \pi x^2 = 6 \pi x (2-x) \\V'(x)=0 \Rightarrow x=2 \\ V(2)= 12 \pi \cdot 2^2 - 2 \pi \cdot 2^3 = 24 \pi - 16 \pi = 8 \pi</math>
Oppgave 6.
a)
Det var 6000 liter i tanken.
1,000 - 0,864 = 0,136 = 13,6%
b)
c)
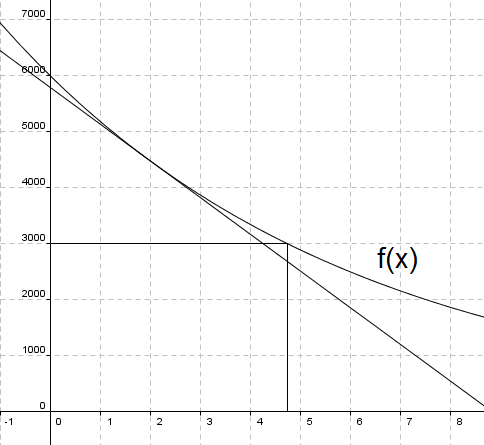
Fra grafen kan man lese at det tar ca. 4 timer og 45 minutter.
d)
Ved å bruke linjal, eller GeoGebra el. kan man legge inn en tangent til grafen i x = 2. Man finner at stigningstallet til grafen er ca. -655. Det betyr at det lekker ut ca. 655 liter fra tanken den andre timen. Av grafen ser man at det vil lekke ut mindre per time etter som tiden går.
Oppgave 7.
a)
<math> T = 2\pi \sqrt{\frac Lg} \\ L= g\left( \frac{T}{2\pi} \right)^2</math>
b)
<math> L= g\left( \frac{T}{2\pi} \right)^2 \\ L= 9,81 m/s^2\left( \frac{1,0s}{2\pi} \right)^2 =0,25m</math>
c)
<math> g = \frac{L}{\left( \frac{T}{2\pi} \right)^2 } \\ g = \frac{10m}{\left( \frac{6,345s}{2\pi} \right)^2} = 9, 806 m/s^2</math>
Oppgave 8.
a)
<math>P(soer troender) = \frac{300000}{5000000}=0,06 = </math> 6%
b)
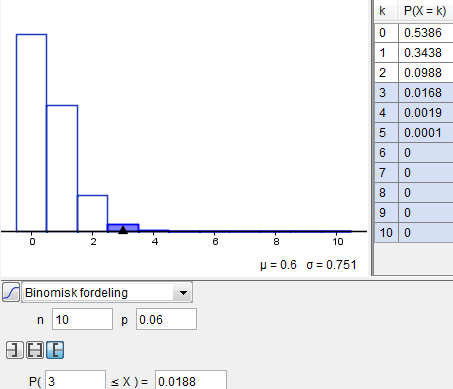
Dette er i utgangspunktet et hypergeometrisk forsøk. Men, fordi utvalget er ekstremt lite i forhold til populasjonen vil sannsynligheten være tilnærmet konstant ved et tilfeldig utvalg av 10 personer. Man kan derfor betrakte dette som et binomisk forsøk.
c)
Sannsynligheten for at ingen av de 10 bor i sørtrøndelag:
<math> P(X=0)= \binom{10}{0} 0,06^0 \cdot 0,94^{10}= 0,539</math>
d)
P(minst 3 bor i Sørtrøndelag)<math> = P(3) + P(4) + P(5) + P(6) + P(7) + P(8) + P(9) + P(10) \approx 0,19</math>
Oppgave 9.
a)
<math>f(x)= a(x-b)^2+c</math>
Fordelen med å skrive en andregradsfunksjon på denne måten er at man får symetrilinjen direkte ved bokstaven b. Bokstaven c gir y-koordinaten til ekstremalpunktet. Bokstavene b og c er forskjellige fra verdiene i utrykket på formen
<math>f(x) = ax^2 +bx +c</math>
Skriver: <math>f(x)= a(x-b)^2+c = A(x-B)^2 +C</math> for ikke å blande konstantene.
<math>f(x)= A(x-B)^2 +C = Ax^2-2ABx+ AB^2+C</math> som gir oss
<math>a =A \\ b= 2AB \\ c = AB^2 +C</math>
Ett nullpunkt:
<math>b^2-4ac=0 \\ (2AB)^2-4A(AB^2+C) = 0 \\ 4A^2B^2 -4A^2B^2 -4AC = 0 \\ C=0</math>
C = 0 gir oss ett nullpunkt, x = B
b)
<math>f'(x) = 0 \\ f'(x) = 2Ax - 2AB \\ 0=6A-2AB \\ 0=2A(3-B) \\ B= 3</math>