Grenseverdier og kontinuitet
Grenseverdi
Grenseverdien til en funksjon er den verdien funksjonsuttrykket går mot når den variable går mot en spesiell verdi.
Vi bruker følgende notasjon:
$\lim\limits_{x \rightarrow a}f(x) =K$
Som leses "limes f av x når x går mot a er k", eller "grensen f beveger seg mot når x går mot a er k".
Eksempel
<math>f(x) = x+2</math>
Dersom x nærmer seg verdien 3 vil f nærme seg verdien 5. Man sier at grenseverdien til f når x går mot 3 er 5. Dett kan man skrive slik:
$\lim\limits_{x \to 3} f(x) = \lim\limits_{x \to 3} x+2 = 5$
lim er en forkortelse for limes som betyr grense på latin.
For å finne grenseverdien til et flerleddet uttrykk, summerer man grenseverdien til de enkelte leddene.
Eksempel:
<math>g(x) = x^2+2x+1</math>
Man ønsker å undersøke hva g går mot når x går mot 3.:
<math>\lim\limits_{x\to3} g(x) = \lim\limits_{x\to3}x^2+2x+1 = 9+6+1 = 16 </math>
Med grenseverdi mener vi den verdi en funksjon f(x) går mot når x går mot et tall, eller mot uendelig.
Når man har brøkuttrykk kan man tilsynelatende få null delt på null som et svar. Null i nevner gir ikke mening og må ommarbeides.
Grenseverdien til en brøkfunksjon der utrykkene i både teller og nevner blir null, finner man ved å faktorisere teller og nevner og forkorte brøken. Eventuelt kan man bruke L’Hopitals regel.
Dersom telleren går mot null og nevneren går mot noe annet, er grenseverdien null.
Dersom nevneren går mot null og teller går mot noe annet har man en vertikal asymptote og ingen grenseverdi.
Eksempel:
<math> \lim\limits_{x\to2}\quad \frac{2x-4}{x^2-2x}= \lim\limits_{x\to2} \quad \frac{2(x-2)}{x(x-2)}= \lim\limits_{x\to2} \quad \frac 2x =1 </math>
Eksempel:
<math>\lim\limits_{x\to1}\quad \frac{x^2-5x+4}{x^2+2x-3} = \lim\limits_{x\to1}\quad \frac{(x-4)(x-1)}{(x+3)(x-1)} = \lim\limits_{x\to1}\quad \frac{(x-4)}{(x+3)} = - \frac 34</math>
Vi forutsetter <math>\lim\limits_{x \rightarrow a}f(x) =K </math> og <math>\lim\limits_{x \rightarrow a}g(x) = L </math>
Generelle sammenhenger <math>\lim\limits_{x \rightarrow a}[f(x) \pm g(x) ] =\lim\limits_{x \rightarrow a}f(x) \pm \lim\limits_{x \rightarrow a}g(x) = K \pm L </math> <math>\lim\limits_{x \rightarrow a}[f(x) \cdot g(x) ] =\lim\limits_{x \rightarrow a}f(x) \cdot \lim\limits_{x \rightarrow a}g(x) = K \cdot L </math> <math>\lim\limits_{x \rightarrow a}\frac{f(x)}{g(x)}= \frac{\lim\limits_{x \rightarrow a}f(x)}{\lim\limits_{x \rightarrow a}g(x)}= \frac KL \quad \quad \quad L\ne 0 </math> <math>\lim\limits_{x \rightarrow a}\frac{1}{f(x)}= \frac{1}{K} \quad \quad \quad K \ne 0 </math> Spesielle sammenhenger <math>\lim\limits_{x \rightarrow 0} \frac{sin x}{x}= 1 </math> <math>\lim\limits_{x \rightarrow 0} \frac{1 - cos x}{x}= 0 </math> <math>\lim\limits_{x \rightarrow \infty}(1 + \frac 1n)^n = e </math> <math>\lim\limits_{x \rightarrow 0}(1 + n)^{\frac 1n} = e </math> <math>For \quad a \geq 1 \quad gjelder \\ \lim\limits_{x \rightarrow + \infty}a^x = + \infty \\ \lim\limits_{x \rightarrow - \infty}a^x = 0</math> <math>For \quad 0 \quad< \quad a \quad< \quad 1 \quad gjelder \\ \lim\limits_{x \rightarrow + \infty}a^x = 0 \\ \lim\limits_{x \rightarrow - \infty}a^x = + \infty </math>
Ensidig grenseverdi
Dersom en funksjon ikke er definert for alle verdier av x, eller den gjør "hopp" i funksjonsverdien kan det være nødvendig å undersøke hva funksjonen går mot når x nærmer seg et tall fra en spesiell side.
<math>\lim\limits_{x \rightarrow a^+}f(x) = K </math>
Uttrykket betyr at f(x) går mot K når x går mot a fra høyre.
<math>\lim\limits_{x \rightarrow a^-}f(x) = R </math>
Uttrykket betyr at f(x) går mot R når x går mot a fra venstre.
Kontinuitet
Dersom grafen til en funksjon er sammenhengende er funksjonene kontinuerlig.
Gitt en funksjon f og et tall k som er med i definisjonsmengden til f. Dersom $\lim\limits_{x \to k}f(x)= f(a)$, da er f kontinuerlig for x = k.
hvilket betyr at
1.f (a) eksisterer, f er definert i a
2.lim f (x) når x går mot a eksisterer
3.verdiene i 1. og 2. er like
Deriverbarhet
Dersom en funksjon ikke er kontinuerlig for x = a, så er funksjonen heller ikke deriverbar for x = a.
Dersom en funksjon er deriverbar for x = a, så er den også kontinuerlig for x = a.
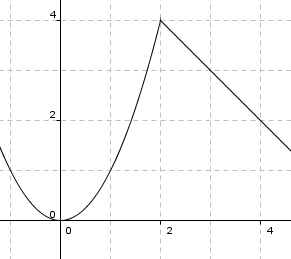
Kontinuerlig men ikke deriverbar for x = 2.
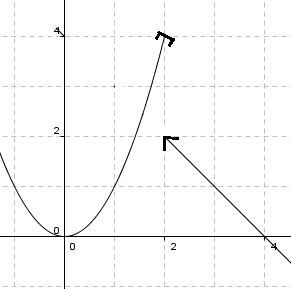
Ikke kontinuerlig eller deriverbar for x = 2