Her kan du stille spørsmål om oppgaver i matematikk på ungdomsskole og barneskole nivå. Alle som føler at de kan bidra er velkommen til å svare.
Moderators: Vektormannen , espen180 , Aleks855 , Solar Plexsus , Gustav , Nebuchadnezzar , Janhaa
Meomeo
Fibonacci
Posts: 3 Joined: 03/12-2019 20:45
28/03-2020 15:53
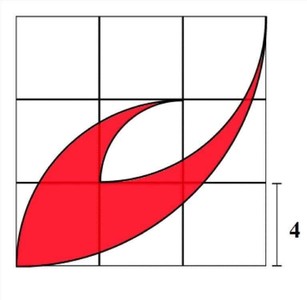
En figur består av kvadrater med sidelengde 4 og kvartsirkler (alle kurvene er kvartsirkler). Finn arealet av den røde figuren - krabbekloen. Forklar din fremgangsmåte.
Trenger hjelp til denne vanskelige! Takk!
Mattebruker
28/03-2020 18:27
Strategi: Finn samla areal av dei kvite felta144 - 36[tex]\pi[/tex] 96 - 16[tex]\pi[/tex] 20[tex]\pi[/tex] - 16 [tex][tex][/tex]areal = 4[tex]^{2}[/tex] = 16[/tex] har vi teke med to gongar.
Kristian Saug
Abel
Posts: 637 Joined: 11/11-2019 18:23
29/03-2020 16:59
Rødt areal = stor klo + liten klo - overlapp =[tex]=32\cdot (\pi -2)[/tex]
Attachments
Krabbeklo.odt (284.73 KiB) Downloaded 444 times