matematikk.net

[tex]\sum_{n=1}^{\infty}\int_{(n-1)\pi}^{n\pi}\frac{\sin(x)}{x}dx[/tex]

Oppgaven er å avgjøre om rekken konvergerer eller divergerer, men jeg forstår ikke hvordan jeg skal gå frem, tror jeg blir skremt av zigmaet og interaltegnet sammen.

Greier du å se hvilket område (n-1)pi til n pi danner med n fra 1 til uendelig?

Nei, dessverre. Prøver, men klarer ikke å integrere.

Summen er bare et nytt integral;

[tex]\sum_{n=1}^{\infty}\int_{(n-1)\pi}^{n\pi}\frac{\sin(x)}{x}dx[/tex]

[tex]= \int_{0}^{\pi}\frac{\sin(x)}{x}dx\; +\; \int_{\pi}^{2\pi}\frac{\sin(x)}{x}dx\; +\; \int_{2\pi}^{3\pi}\frac{\sin(x)}{x}dx\; + \; \ldots[/tex]

[tex]= \int_{0}^{\infty}\frac{\sin(x)}{x}dx[/tex]

Nå kan du teste om det konvergerer eller ikke.

edit; en enkel måte å visualisere summen på

Her er grafen til [tex]y=\frac{\sin(x)}{x}[/tex]



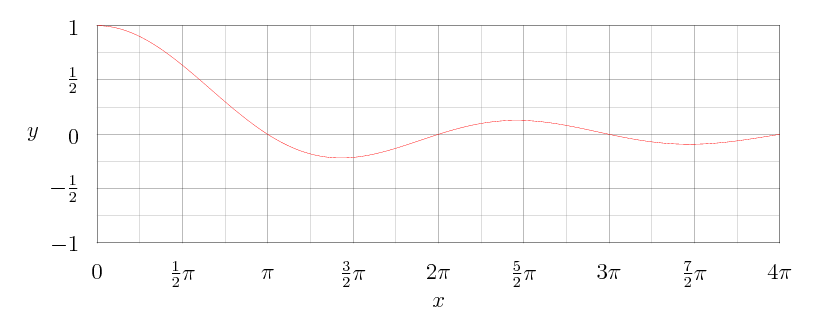
Vi ser fra integralet at den første delsummen er arealet fra [tex]y[/tex] til [tex]x[/tex] med [tex]x[/tex] mellom [tex]0[/tex] til [tex]\pi[/tex].

Hvis vi lar arealer under [tex]x[/tex]-aksen være negative så får vi de andre delsummene til å bli arealet fra [tex]y[/tex] til [tex]x[/tex] med [tex]x[/tex] mellom [tex](n-1)\pi[/tex] til [tex]n\pi[/tex], på grafen blir da de fire første delsummene vist.

Vi ser da enkelt at hele summen er arealet fra [tex]y[/tex] til [tex]x[/tex] med [tex]x[/tex] mellom [tex]0[/tex] til [tex]\infty[/tex].

Bruk alternerende-rekke-testen. Dette er en alternerende rekke hvor leddene går mot null, som medfører at den konvergerer.

Takk for hjelpen.