Oppgave 1

Oppgave 2

takk!
Moderators: Vektormannen, espen180, Aleks855, Solar Plexsus, Gustav, Nebuchadnezzar, Janhaa
dizzy wrote:Tips!
m=int,t=a..b),abs(r'(t))*rho(t)dt gir m= 8*Pi^2*sqrt(2)

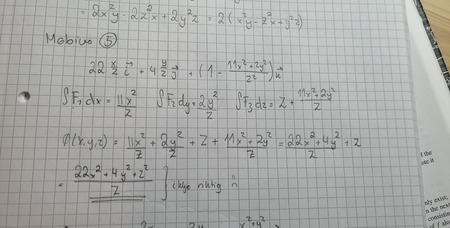

hva mener du med at den ene faller bort? når man gjør som innlegget over, integrerer man jo komponentene av F. Når kommer deriveringen mhp den andre inn?atlebjarnebob wrote:Tror du eventuelt kan skrive "C(y) + C(z)" i stedet for "C(y,z)", og så regne ut hver av de for seg selv slik som ved to variabler (den ene vil jo da falle bort når du deriverer med hensyn på den andre). Fikk selv riktig svar på den måten ihvertfall.

Skal ikke si at jeg har skjønt det helt 100% selv, men her er ihvertfall tankegangen min (se bilde for utregning):VektorFelt wrote:hva mener du med at den ene faller bort? når man gjør som innlegget over, integrerer man jo komponentene av F. Når kommer deriveringen mhp den andre inn?atlebjarnebob wrote:Tror du eventuelt kan skrive "C(y) + C(z)" i stedet for "C(y,z)", og så regne ut hver av de for seg selv slik som ved to variabler (den ene vil jo da falle bort når du deriverer med hensyn på den andre). Fikk selv riktig svar på den måten ihvertfall.