matematikk.net

Tre sirkler med sentrum S[sub]1[/sub], S[sub]2[/sub] og S[sub]3[/sub] og radius r tangerer hverandre. S[sub]1[/sub], S[sub]2[/sub] og S[sub]3[/sub] danner trekant T[sub]1[/sub]. T[sub]2[/sub] er slik at sidene tangerer sirkelperiferiene. Finn forholdet mellom arealet av trekantene. (Dvs. T[sub]2[/sub]/T[sub]1[/sub].)

Hvis alle sirklene har samme radius må trekantene være likesidet, og den innerste trekanten ha sidelengde [tex]2r[/tex] og arealet blir [tex]A_1=\sqrt{3}r^2[/tex]. Hvis vi lar sentrum av [tex]T_1[/tex] være origo, kan man finne midtpunktene til sidene til den store trekanten.

[tex]\vec{S_1O}=\left[r,\frac{\sqrt{3}}{3}r\right] \\ M_1=\vec{OS_1}+[r,-r]=\left[0,-\frac{\sqrt{3}+3}{3}r\right][/tex]

Nå vet jeg avstanden fra sentrum til sidene av den store trekanten. Forholdet mellom sidelengdene og anstanden mellom sentrum og sidene er [tex]A_s=\frac{\sqrt{3}}{6}s[/tex], der [tex]A_s[/tex] er anstanden og [tex]s[/tex] er sidelengden. Vi omformer dette til [tex]\frac{6}{\sqrt{3}}A_s=s[/tex] og setter ditte inn i vår problemstilling. Vi får at

[tex]s=\frac{6}{\sqrt{3}}\cdot \frac{\sqrt{3}+3}{3}r=\frac{6\sqrt{3}+18}{3\sqrt{3}}r[/tex]. Nå kjører vi dette gjennom "arealformelen" og får at [tex]A_2=\frac{\sqrt{3}}{4}\left(\frac{6\sqrt{3}+18}{3\sqrt{3}}r\right)^2=(4\sqrt{3}+6)r^2[/tex] og forholdet blir

[tex]\frac{A_1}{A_2}=\frac{4\sqrt{3}+6}{sqrt{3}}=\underline{\underline{4+2\sqrt{3}}}[/tex]


Ble det riktig, eller ei?

Jeg får det samme, med denne fremgangsmåten:

Trekantene er formlike. Forholdet mellom sidene er da et tall k, og forholdet mellom arealet blir da k[sup]2[/sup]. Det er altså bare til å finne k. Trekantene her er 30-60-90-trekanter, siden hypotenusen (2r) er dobbelt så lang som den korteste kateten (r). Et bilde sier mer enn tusen ord:



Deler altså opp linjestykket fra det ene hjørnet til midtpunktet i den store trekanten i tre deler. Bruker så formlikhet og at lengdeforholdene i 30-60-90-trekanter er [tex]1 : \sqrt 3 : 2[/tex] til å finne lengdene av disse delene. Den første delen er jo bare lik r, den neste er hypotenus i en 30-60-90-trekant med lengste katet r som gir lengden [tex]\frac{2}{sqrt 3}r[/tex], og den siste er minste katet i en 30-60-90-trekant med lengste katet r som gir lengden [tex]\frac{1}{\sqrt 3}r[/tex]. Samlet lengde av linjestykket blir da [tex]\frac{1}{sqrt 3}r + \frac{2}{\sqrt 3}r + r[/tex]. Forholdstallet mellom denne og tilsvarende side i T[sub]1[/sub] blir da [tex]k = \frac{\frac{1}{sqrt 3}r + \frac{2}{\sqrt 3}r + r}{r} = \frac{1}{sqrt 3} + \frac{2}{\sqrt 3} + 1 = 1 + \frac{3}{sqrt 3} = 1 + \sqrt 3[/tex]. Da blir [tex]k^2 = (1 + \sqrt 3)^2 = 1 + 2\sqrt 3 + 3 = \underline{\underline{4 + 2\sqrt 3}}[/tex]

Vektormannen skrev:Et bilde sier mer enn tusen ord:

Med mindre det er et bilde av ett ord.

Oppgaven er forresten en modifisert abeloppgave fra 1993.

Her er min løsning folkens:

Vi vet at forholdene mellom to samsvarende linjestykker opphøyd i andre er like forholdene mellom arealene til figurene.

Som vektormannen sier, så er det enklere å forklare dette med bilde:



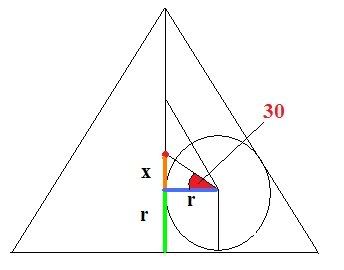
[tex]{(\frac{x+r}{x})}^2=\text{forhold mellom trekantene}\\{(\frac{x^2+r^2+2xr}{x^2})}[/tex]

Vi finner et utrykk for x:

[tex]\frac{x}{r}=tan 30\\x=r\cdot tan 30\\x=r \cdot \frac{\sqrt{3}}{3}[/tex]

Vi setter inn for [tex]x[/tex]:

[tex]{\frac{{(r \cdot \frac{\sqrt{3}}{3}})^2+r^2+2(r \cdot \frac{\sqrt{3}}{3})r}{(r \cdot \frac{\sqrt{3}}{3})^2}=\\{\frac{{(r^2 \cdot \frac{{3}}{9}})+r^2+2(r^2 \cdot \frac{\sqrt{3}}{3})}{{(r^2 \cdot \frac{{3}}{9}})}}=\\{\frac{{(\frac{{r^2}}{3}})+\frac{3r^2}{3}+\frac{2(r^2 \cdot {\sqrt{3}})}{3}}{{(\frac{{r^2}}{3}})}}=\\\frac{r^2+3r^2+2 \cdot r^2 \cdot \sqrt{3}}{r^2}=\\\frac{r^2{(1+3+2 \sqrt{3})}}{r^2}=1+3+2\sqrt{3}=4+2\sqrt{3}[/tex]