Page 1 of 1
square and circles
Posted: 27/02-2020 16:47
by Janhaa
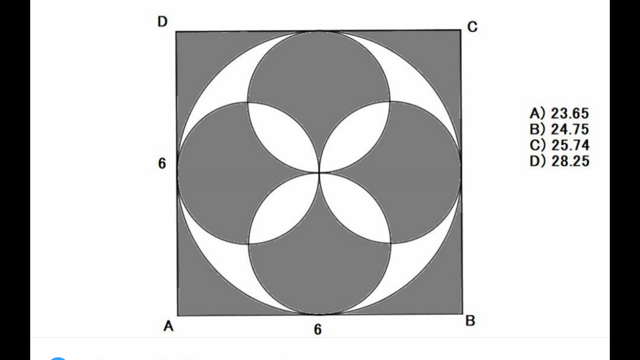
- square-and-circles.PNG (252.84 KiB) Viewed 8658 times
Finn det svarte arealet?
Re: square and circles
Posted: 27/02-2020 21:43
by Mattebruker
Ser ut til å vere lita interesse for dette problemet. Tillet meg difor å levere eit bidrag for om mogleg å få ein respons:
Areal( dark area ) = Areal ( fire småsirklar med radius r = [tex]\frac{3}{2}[/tex] ) - Areal ( 8 sirkelsegment ) + Areal ( 4 "hjørne" i kvadratet ABCD ( s = 6 ) ) = 45 - [tex]\frac{9\pi }{2}[/tex]
Re: square and circles
Posted: 27/02-2020 22:44
by josi
Havnet på $54-9\pi = 25.73$ som synes ganske nær alternativ C.
Re: square and circles
Posted: 27/02-2020 23:53
by Kristian Saug
Omgjort! Jeg havner på samme svar som josi.
Areal(dark) = Areal(kvadrat - stor sirkel + 4 små sirkler - 4 sirkelsegment pr liten sirkel)
[tex]6^{2}-\Pi \cdot 3^{2}+4\cdot \Pi \cdot 1,5^{2}-8\cdot 1,5^{2}\cdot (\frac{\Pi }{2}-1)=54-9\Pi[/tex] ([tex]\approx 25,73[/tex])
Hver segment-del er [tex]\frac{1}{4}\cdot \Pi \cdot 1,5^{2}-\frac{1}{2}\cdot 1,5^{2}=\frac{1}{2}\cdot 1,5^{2}\cdot (\frac{\Pi }{2}-1)[/tex].
Og hver liten sirkel "mister" jo 4 slike segmenter! Altså 16 tilsammen. Det var det fiffige ved oppgaven! Fort gjort å gå i en felle der!
En takk til janhaa som publiserte denne oppgaven. Fin for noen og enhver, fra ungdomsskole til videregående og høgskole. Og for lærere!
Re: square and circles
Posted: 02/03-2020 18:49
by Janhaa
Kristian Saug wrote:Omgjort! Jeg havner på samme svar som josi.
Areal(dark) = Areal(kvadrat - stor sirkel + 4 små sirkler - 4 sirkelsegment pr liten sirkel)
[tex]6^{2}-\Pi \cdot 3^{2}+4\cdot \Pi \cdot 1,5^{2}-8\cdot 1,5^{2}\cdot (\frac{\Pi }{2}-1)=54-9\Pi[/tex] ([tex]\approx 25,73[/tex])
Hver segment-del er [tex]\frac{1}{4}\cdot \Pi \cdot 1,5^{2}-\frac{1}{2}\cdot 1,5^{2}=\frac{1}{2}\cdot 1,5^{2}\cdot (\frac{\Pi }{2}-1)[/tex].
Og hver liten sirkel "mister" jo 4 slike segmenter! Altså 16 tilsammen. Det var det fiffige ved oppgaven! Fort gjort å gå i en felle der!
En takk til janhaa som publiserte denne oppgaven. Fin for noen og enhver, fra ungdomsskole til videregående og høgskole. Og for lærere!
Bra, helt riktig. Ja, artig oppgave som passer for flere trinn.