Side 1 av 2
Omsirkel-nøtt
Lagt inn: 08/04-2022 20:29
av LAMBRIDA
![Bilde]()
Kvadratet har sider på 10 cm, mens kvartsirklene har radius 5 cm. Hvilken radius har den omskrevne sirkel?
Re: Omsirkel-nøtt
Lagt inn: 08/04-2022 22:16
av Mattebruker
Anta at dei to "prikkane" på den øverste kvartsirkelen avgrensar ein boge på v grader ( går ut frå at prikken til venstre ligg på omsirkel )
Da er radien til omsirkel = 10 - 5 tanv
Re: Omsirkel-nøtt
Lagt inn: 09/04-2022 14:24
av Mattebruker
Vinkelen v eg viste til i mitt første innlegg må oppfylle likninga
5 + [tex]\frac{5}{cosv}[/tex] = 10 - 5 tanv , v [tex]\in[/tex] [ 0 , 45[tex]^{0}[/tex] [tex]>[/tex]
Denne likninga har berre ei løysing : v = 0
Svar: Radius( omsirkel ) = 5 + [tex]\frac{5}{cos0}[/tex] = 10 - tan0 = 10
Re: Omsirkel-nøtt
Lagt inn: 11/04-2022 12:50
av Solar Plexsus
Vi setter inn et koordinatsystem der origo er skjæringspunktet mellom diagonalene i kvadratet.
Likningen for den omskrevne sirkelen er
$(1) \;\; (x - a)^2 + (y - b)^2 = r^2$,
der $(a,b)$ er sentrum og $r$ er radius i den omskrevne sirkelen.
Vi ser vi at punktene $(10,0), (0,10), (-5,-5)$ ligger på den omskrevne sirkelen. Ergo må ifølge likning (1)
$(2) \;\; (10 - a)^2 + b^2 = r^2$,
$(3) \;\; a^2 + (10 - b)^2= r^2$,
$(4) \;\; (a + 5)^2 + (b + 5)^2 = r^2$.
Ved å trekke likning (2) fra likning (3), får vi $20(a - b) = 0$, i.e. $a=b$, som innsatt i likning (3) og (4) gir oss
$(5) \;\; 2a^2 - 20a + 100 = r^2$,
$(6) \;\; 2a^2 + 20a + 50 = r^2$.
Ved å trekke likning (5) fra likning (6), får vi $40a - 50 = 0$. Altså er ${\textstyle a = \frac{5}{4}}$, som insatt i likning (6) gir
${\textstyle r^2 = 2(\frac{5}{4} + 5)^2 = 2 \cdot (\frac{25}{4})^2}$,
som medfører at
${\textstyle r = \frac{25}{2\sqrt{2}}}$.
Re: Omsirkel-nøtt
Lagt inn: 11/04-2022 16:29
av Mattebruker
Ryddig og strukturert løysing v/ Solar Plexus. Vedlegget til oppgåva ( figuren ) kan mistydast. Det burde vore presisert i oppgaveteksta at den øverste kvartsirkelen og omsirkel har to fellespunkt ( ingen fellestangent ).
Re: Omsirkel-nøtt
Lagt inn: 11/04-2022 22:36
av LAMBRIDA
Denne løsningen var nær, men ikke helt etter det eksakte svaret.
Re: Omsirkel-nøtt
Lagt inn: 11/04-2022 22:48
av Janhaa
LAMBRIDA skrev: ↑11/04-2022 22:36
Denne løsningen var nær, men ikke helt etter det eksakte svaret.
Han har jo et eksakt svar. Hva er ditt eksakte svar?
Kan du ikke vise full utregning så vi får se….
Re: Omsirkel-nøtt
Lagt inn: 11/04-2022 23:02
av LAMBRIDA
Eg skal prøva å visa det eksakte svaret og den måten eg regner på. Det er ikke likninger, men et bevis på at svaret mitt er rett. Eg skal prøva på dette i morgen.
Re: Omsirkel-nøtt
Lagt inn: 12/04-2022 13:40
av Janhaa
LAMBRIDA skrev: ↑11/04-2022 22:36
Denne løsningen var nær, men ikke helt etter det eksakte svaret.
Du blander ikke med denne;
[tex]r=\frac{25\sqrt{2}}{4}[/tex]
?
Re: Omsirkel-nøtt
Lagt inn: 12/04-2022 13:54
av LAMBRIDA
Det eksakte uttrykket på radien til omsirkelen: 5/3(2[tex]\sqrt{10}-1) =8,874258867 cm[/tex]
Linjestykket EF går fra F, gjennom B og S og treffer E vinkelrett på AC. Den rettvinkla og likebente trekanten ABC har 45 grader både i A og C, mens den har 90 grader i B. SF, SA og SC er radien til omsirkelen.
SF(8,87425)-BF(5)= BS(3,87425). EB(7,90569415)-BS(3,87425)=SE(4,03144415)
Høyden i trekanten ABS og CBS: BS(3,87425*sin 45 =2,739508447 cm.
Shift sin 2,73950844/8,87425 =17,98109039 grader
Shift sin 4,03144415/8,87425 = 27,01897908 grader
Summen av de to vinklene her blir 45 grader, som er vinkelgradene i A og C. Det betyr at radien på omsirkelen er rett med det eksakte uttrykket eg har vist. Ellers hadde vi ikke fått summen 45 grader, som vi vet at vinkelgradene er i A og C.
![Bilde]()
Re: Omsirkel-nøtt
Lagt inn: 12/04-2022 14:32
av Mattebruker
Kommentar:
Dersom C er einaste fellespunkt mellom omsirkel og kvartsirkel ( del av halvsirkel ) , må radien CS gå langs radien til kvartsirkel i punktet C ettersom desse
sirklane da får ein fellestangent i dette punktet( C ). Uansett greier eg ikkje å sjå at [tex]\bigtriangleup[/tex]ACB er likebeina og rettvinkla.
Re: Omsirkel-nøtt
Lagt inn: 12/04-2022 17:49
av Janhaa
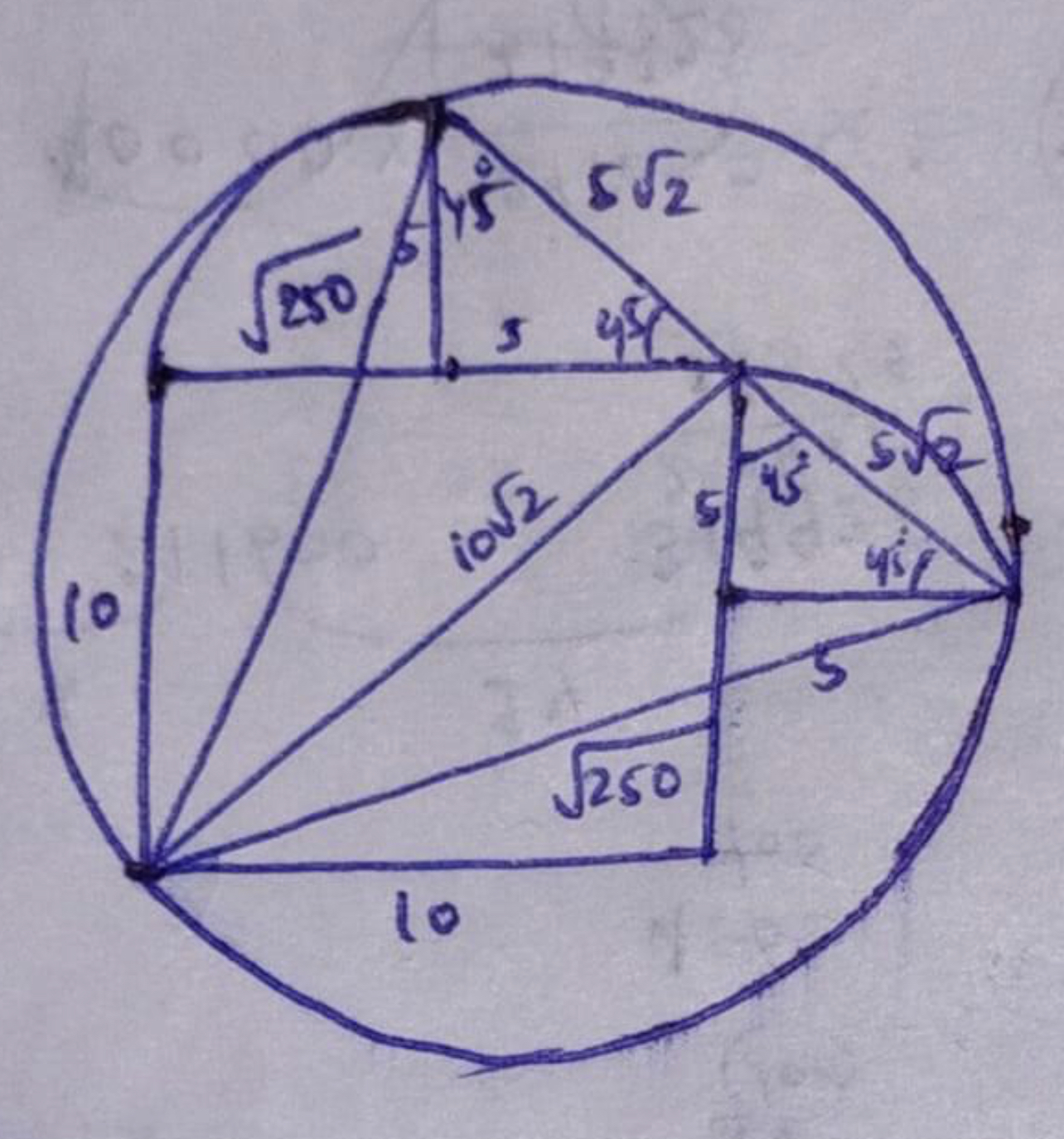
- A5419550-DA65-43E8-AA4E-3D37C5B7E8E9.jpeg (1.03 MiB) Vist 5982 ganger
Bruker formel for omskreven sirkel direkte:
[tex]R = \frac{a*b*c}{4*triangle\,\, Area }=\frac{\sqrt{250}\sqrt{250}*10*\sqrt{2}}{4*0.5*10\sqrt{2}*10\sqrt{2}}=25/(2\sqrt{2})=(25\sqrt2)/4[/tex]
Re: Omsirkel-nøtt
Lagt inn: 13/04-2022 10:42
av Mattebruker
Kontrollrekning:
Viser til Janhaa sitt innlegg som verifiserer Solar Plexus si løysing.
Den innskrivne trekanten er likebeina med sider [tex]\sqrt{250}[/tex], [tex]\sqrt{250}[/tex] og 10[tex]\sqrt{2}[/tex]
Lat 2[tex]\alpha[/tex] vere vinkelen mellom dei like lange sidene .
Da er sin( 2[tex]\alpha[/tex] ) = 2 [tex]\cdot[/tex] sin( [tex]\alpha[/tex] ) [tex]\cdot[/tex] cos( [tex]\alpha[/tex] ) = 2[tex]\cdot[/tex] [tex]\frac{5\sqrt{2}}{5\sqrt{10}}[/tex][tex]\cdot[/tex][tex]\frac{10\sqrt{2}}{5\sqrt{10}}[/tex] = [tex]\frac{4}{5}[/tex]
Finn radius R i omskriven sirkel.
Sinusproporsjonen for trekant gir
2 R = ( side i trekanten )/ ( sinus til motståande vinkel ) = [tex]\frac{10\sqrt{2}}{\frac{4}{5}}[/tex] = [tex]\frac{25}{2}[/tex][tex]\sqrt{2}[/tex] [tex]\Rightarrow[/tex] R = [tex]\frac{25}{4}[/tex][tex]\sqrt{2}[/tex]
Lambrida og Mattebruker lot seg "forføre" av vedlegget til oppgåva ( figuren ) som indikerer at øverste kvartsirkel tangerer omsirkel. Slik er det openbart ikkje.
Dei to objekta har to fellespunkt og dermed ingen fellestangent. Sentrum S i omsirkel kan derfor ikkje ligge på forlenginga av radien FB ( sjå skisse v/ Lambrida )
Re: Omsirkel-nøtt
Lagt inn: 13/04-2022 21:52
av LAMBRIDA
Eg har jo vist dere det eksakte svaret.
Re: Omsirkel-nøtt
Lagt inn: 13/04-2022 23:57
av Gustav
Virker som det har vært noen misforståelser av oppgaven(?) Generelt vil 3 punkter i planet (som ikke ligger på en linje) definere en entydig sirkel, og her tolker jeg det som at den omskrevne sirkelen er definert av punktet til høyre, et av hjørnene i kvadratet, samt det felles tangeringspunktet mellom den øvre kvartsirkelen og den største sirkelen. I så fall stemmer det ikke at punkt (0,10) ligger på den omskrevne sirkelen (ref. Solar plexus sitt innlegg)