Globale maksimum/minimum

[Jeppe214]

Hei, jeg bare lurte på noe, jeg har en funksjon her hvor jeg skal finne globale maks og min og deres verdier(dersom de eksisterer) og har fått dette:



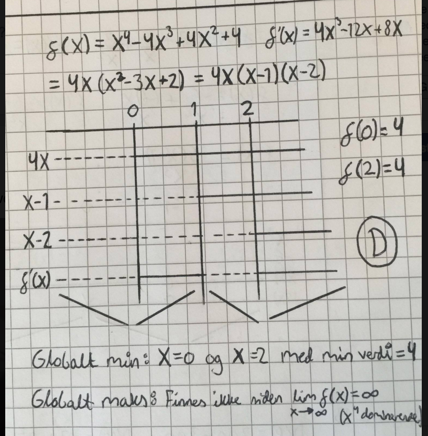
Tenker jeg riktig hvis jeg sier det slik:

Når f(x) går mot positiv evig så får vi "evig" positivt tall, ERGO ingen global maksverdi.

Når f(x) går mot negativ evig, så får vi fremdeles et "evig" positivt tall, som bare betyr at vi fremdeles ikke har noen maksverdi, dermed MÅ en eller begge av de lokale minimumspunktene (her 0 og 2) være de globale minimumspunktene.

Og får å regne ut minimumsverdiene regner jeg rett og slett ut f(2)=4 og f(0)=4 og finner da ut at globalt min er da både x=0 og x=2 fordi begge gir lik verdi (4)

[Aleks855]

Ja, det høres riktig ut.

Men når du sier "punkt" så er det viktig å understreke at et punkt vil bestå av en x- og en y-verdi. Det vil si at et punkt er på formen $(x, y)$ eller $(x, f(x))$ her.

Så når du sier punktet $x = 2$ så gir ikke det så mye mening, fordi $x = 2$ er ei vertikal linje, og ikke et punkt.

De globale minimumspunktene er $(0, 4)$ og $(2, 4)$.

Dette er selvfølgelig småpirk i det store bildet, men burde være fordøyelig siden du ser ut til å ha kontroll på det andre.

Vi kan også utvide svaret fra $\lim\limits_{x\to\infty}f(x) \to\infty$ til å inkludere også når x går mot minus uendelig: $\lim\limits_{x\to\pm\infty}f(x) \to\infty$

[Jeppe214]

Aha! Det lå et sted inn i hjernen min, men når du forklarte det slik ble det mye lettere å forstå det! Tusen takk for svar