Posted: 26/10-2011 09:22


Min kommentar:Razzy wrote:Rettelse - b)Vektormannen wrote:Jada, er enig i metoden, men det ser ut som du har gjort en eller annen regnefeil. Ingen av komponentene i normalvektoren skal bli 0! (Det ser vi fra figuren også.)
Fant feilen: Normalvektoren skal være: [tex]$$\vec {BC}X\vec{BD} = 16\left[ {2,2,1} \right]$$[/tex]
[tex]$$B\left( {4,0,0} \right)$$[/tex]
[tex]$$\alpha:\;a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) + c\left( {z - {z_0}} \right)=0$$[/tex]
[tex]\alpha:\;32\left( {x - {4}} \right) + 32\left( {y - {0}} \right) + 16\left( {z - {0}} \right)=0[/tex]
[tex]$$\alpha:\;32x - 128 + 32y + 16z = 0$$[/tex]
[tex]\underline{\underline{\alpha:\;16\left[ {2x + 2y + z - 8} \right] = 0}}[/tex]
Kommentar: Dette så litt bedre ut; hvordan visse du at jeg hadde regnet feil? Hvordan visste du at den andre normalvektoren jeg fant ikke var riktig? ("jeg bare regner jeg" )
Punktene til skjæringspunktet er ikke jeg heller så fortrolig medRazzy wrote:Kommentar: Er ikke helt fortrolig med punktene til skjæringspunktet, føler på meg at disse burde vært mer heltall? Kan jeg gange ut 9? Det går vel ikke... - men det nærmer seg!
Skrev punktene, mente koordinatene. Flott dere passer på meg her, nå begynner jeg å få ting på plass.mstud wrote:Punktene til skjæringspunktet er ikke jeg heller så fortrolig med(det kan jeg godt forstå du ikke er) , koordinatene til skjæringspunktet er en litt annen sak ...
Har ikke kontrollert utregningen din i c), men nå har du jo uansett tenkt å regne c) en gang til...
Det er i hvert fall ikke alltid man får heltall i vektoroppgaver etter hvert, ta det som et kompliment hvis ikke, det betyr bare at du holdes for å være en mer "avansert" vektorregner enn de som bare får oppgaver med heltall. Altså at de regner med at du klarer en vektoroppgave med brøker i utregningen...
[tex](\frac{16}{9}, \frac{16}{9}, \frac{8}{9}) \Leftrightarrow (\frac{2}{9}, \frac{2}{9}, \frac{1}{9})[/tex]Vektormannen wrote:Du har jo allerede funnet ut at skjæringspunktet er [tex](\frac{16}{9}, \frac{16}{9}, \frac{8}{9})[/tex]! Det gjorde du jo i oppgave c), og det svaret var riktig. Når du gjorde det samme igjen nå nettopp så var det helt riktig frem til du skrev: [tex](\frac{16}{9}, \frac{16}{9}, \frac{8}{9}) \Leftrightarrow (\frac{2}{9}, \frac{2}{9}, \frac{1}{9})[/tex]. Hva mener du med det? Det du skrev før pilen er jo akkurat samme punkt som du fant i går, og det er riktig, men hva mener du med ekvivlanespilen?
Edit: Ja, det er helt riktig at avstandsformelen bare er lengden av vektoren mellom punktene. Det er helt riktig regnet, med unntak av at punktet S du har brukt er galt (som forklart ovenfor.)
Selvfølgelig er det det - altså er man i tvil angående koordinatene til et evt skjæringspunkt (og man har ligningen for planet som jeg hadde) - sett dem inn å sjekk om det stemmer!Vektormannen wrote:Som sagt, skjæringspunktet [tex](\frac{16}{9}, \frac{16}{9}, \frac{8}{9})[/tex] er riktig det. Hvis man er i tvil er det jo bare å sjekke ved å sette inn i planligningen og se om den blir oppfylt:
[tex]2 \cdot \frac{16}{9} + 2 \cdot \frac{16}{9} + \frac{8}{9} - 8 = \frac{32 + 32 + 8}{9} - 8 = \frac{72}{9} - 8 = 8 - 8 = 0[/tex]
Altså passer punktet inn i planet, og fra før vet vi det ligger på linja. Da må det være riktig skjæringspunkt.
Hm ja, oppga du hvor langt punktet var daRazzy wrote:...
[tex](\frac{16}{9}, \frac{16}{9}, \frac{8}{9}) \Leftrightarrow (\frac{2}{9}, \frac{2}{9}, \frac{1}{9})[/tex]Vektormannen wrote:Du har jo allerede funnet ut at skjæringspunktet er [tex](\frac{16}{9}, \frac{16}{9}, \frac{8}{9})[/tex]! Det gjorde du jo i oppgave c), og det svaret var riktig. Når du gjorde det samme igjen nå nettopp så var det helt riktig frem til du skrev: [tex](\frac{16}{9}, \frac{16}{9}, \frac{8}{9}) \Leftrightarrow (\frac{2}{9}, \frac{2}{9}, \frac{1}{9})[/tex]. Hva mener du med det? Det du skrev før pilen er jo akkurat samme punkt som du fant i går, og det er riktig, men hva mener du med ekvivlanespilen?
Edit: Ja, det er helt riktig at avstandsformelen bare er lengden av vektoren mellom punktene. Det er helt riktig regnet, med unntak av at punktet S du har brukt er galt (som forklart ovenfor.)
Nå skal jeg forklare deg hva jeg tenkte: Det er ikke vits å oppgi skjæringspunktet "16 ganger lengre enn det egentlig er"...
Jeg skjønner når jeg forklarer deg dette at jeg har tenkt helt feil; et skjæringspunkt er konstant! Det forandres ikke - det jeg har tenkt er vektor.
...
Liten konklusjon: Bruk fornuft i regning - kanskje spesielt lett ved regning av vekorer. Drøft evt svar og se om de er fornuftige og kontroller svar der det er mulig (ved å sette inn i ligningene)
Jeg bare oppga hvor punktet befant seg - ikke hvor "langt" det var?mstud wrote:Hm ja, oppga du hvor langt punktet var da
Mente at det er spesielt lett fordi man har en mulighet til å se for seg hva man gjør (feks slik du kunne fortelle at den første normalvektoren jeg fant kun gikk langs z-akse og dermed var feil).mstud wrote:Hva mener du med at det kanskje er spesielt lett å bruke fornuft ved regning av vektorer? Personlig synes jeg det er en av de vanskeligste regnemåtene å bruke fornuft på underveis. Fornuften må vanligvis heller komme inn etterpå og sjekke resultatet, det er i hvert fall min erfaring...
Thanks m8mstud wrote:"Bruk fornuft i regning... Drøft evt svar og se om de er fornuftige og kontroller svar der det er mulig (ved å sette inn i ligningene)" Flott konklusjon! Både for vektorregning o.a. regning.

Du er litt av en tenker du mstud - og det er det som gjør deg/oss/alle som har gjort det bra i livet til noe!mstud wrote:Jepp, bare hvor punktet var, og i matematisk betydning er et punkt et punkt og har "ingen" lengde (vanligvis). F.eks. er arealet av et punkt et punkt. (f.eks. som en pixel), men vi oppgir ikke lengde fordi et punkt er egentlig den minste "prikken" man kan få til, og er altså bare definert ved plassering, ikke størrelse, for størrelsen av et punkt er bare "et punkt"-størrelse. Det var dette jeg siktet til med sprsmålet mitt om hvor langt punktet ditt var ... (Ikke så veldig viktig, men kanskje du da ikke tenker på lengden av et punkt en annen gang) Et punkt man kan oppgi størrelsen til er i grunnen heller en prikk/flekk enn et punkt.
Ja, men når du regnet ut [0,0,16] som vektorprodukt, måtte du bruke fornuft til å tenke på vektoren tegnet i koordinatsystemet etter at du hadde regnet ut kryssproduktet... Det ville ikke hjelpe å tenke på normalvektoren til planet i koordinatsystemet underveis i regningen men du kunne bruke det til å se om det ferdig utregnede kryssproduktet var riktig/feil.
Men ja, det er absolutt riktig at tegningen hjelper til med å sjekke svar i vektorregning, fordi man får en visualisering av situasjonen. (Litt verre å tegne i n-dimensjoner enn i 3, så der har det gjerne ikke så stor funksjon, men men vi er nå ikke kommet til det enda) Figurer som skaper flere problemer, ja de bør man kanskje ikke tegne?
(er med på den)
Er vel i grunnen ikke bare ingeniører det gjelder? De færreste har vel fordel av å handle i blinde, eller? (Se f.eks. for deg en sykepleier/lege som arbeider i blinde, tror ikke jeg ville vært pasient da, hehe)
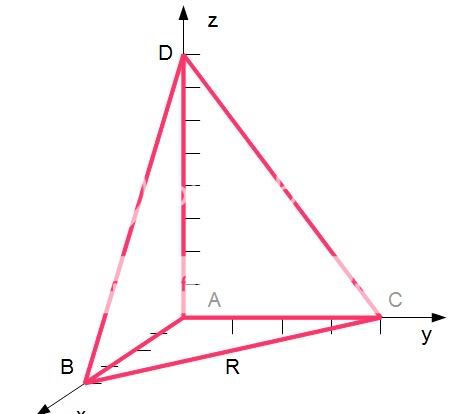
Jeg er i alle fall enig i figurene...Razzy wrote:Forslag til deloppgave d
opprinnelige figur
figur etter velt
Hva mener du her? Opprinnelig var avstanden mellom origo og A 0, siden A lå i origo, hvor har du opplyst en avstand etter veltet?Razzy wrote: Vi kjenner avstanden fra origo til A, og denne avstanden vil være den samme som fra planet alfra eller punktet R med koordinatene: [tex]$$R\left( {2,2,0} \right)$$[/tex] - til den nye lokasjonen til A.
Riktig utregning, bortsett fra at [tex]\sqrt{(-z)^2}=\frac 13 \Leftrightarrow -z=\frac 13 \Leftrightarrow z=-\frac 13[/tex]. Du fant vel [tex]|\vec{AR} |[/tex] ut i fra a og R i forrige oppgave håper jeg... Men da er [tex]|\vec{AR} |=\sqrt {2^2+2^2+0^2}=2\sqrt 2[/tex] siden [tex]\vec{AR}=[2,2,0][/tex] Fra A (0,0,0) til R(2,2,0)...Razzy wrote: Det nye punktet A befinner seg altså rett ovenfor punktet R og har derfor koordinatene: [tex]$$A\left( {2,2,z} \right)$$[/tex]
Vi løser resten av oppgaven algebraisk:
[tex]$$\vec{AR} = \left[ {2 - 2,2 - 2,0 - z} \right] = \underline {\left[ {0,0, - z} \right]} $$[/tex]
[tex]$$\left| {\vec{AR} } \right| = {1 \over 3}$$[/tex]
[tex]$$\sqrt {{0^2} + {0^2} + {{\left( { - z} \right)}^2}} = {1 \over 3}$$[/tex]
[tex]$$\underline{\underline {z = {1 \over 3}}} $$[/tex]
Kommentar Enig i min tolkning av deloppgave d?
For å sitere:Razzy wrote:Du er litt av en tenker du mstud - og det er det som gjør deg/oss/alle som har gjort det bra i livet til noe!mstud wrote:Jepp, bare hvor punktet var, og i matematisk betydning er et punkt et punkt og har "ingen" lengde (vanligvis). F.eks. er arealet av et punkt et punkt. (f.eks. som en pixel), men vi oppgir ikke lengde fordi et punkt er egentlig den minste "prikken" man kan få til, og er altså bare definert ved plassering, ikke størrelse, for størrelsen av et punkt er bare "et punkt"-størrelse. Det var dette jeg siktet til med sprsmålet mitt om hvor langt punktet ditt var ... (Ikke så veldig viktig, men kanskje du da ikke tenker på lengden av et punkt en annen gang) Et punkt man kan oppgi størrelsen til er i grunnen heller en prikk/flekk enn et punkt.
Ja, men når du regnet ut [0,0,16] som vektorprodukt, måtte du bruke fornuft til å tenke på vektoren tegnet i koordinatsystemet etter at du hadde regnet ut kryssproduktet... Det ville ikke hjelpe å tenke på normalvektoren til planet i koordinatsystemet underveis i regningen men du kunne bruke det til å se om det ferdig utregnede kryssproduktet var riktig/feil.
Men ja, det er absolutt riktig at tegningen hjelper til med å sjekke svar i vektorregning, fordi man får en visualisering av situasjonen. (Litt verre å tegne i n-dimensjoner enn i 3, så der har det gjerne ikke så stor funksjon, men men vi er nå ikke kommet til det enda) Figurer som skaper flere problemer, ja de bør man kanskje ikke tegne?
(er med på den)
Er vel i grunnen ikke bare ingeniører det gjelder? De færreste har vel fordel av å handle i blinde, eller? (Se f.eks. for deg en sykepleier/lege som arbeider i blinde, tror ikke jeg ville vært pasient da, hehe)
Drøft, still spørsmål, finn ut hvorfor ting er som de er. Kommer garantert til å humre for meg selv hvis jeg begynner å tenke lengde av et punkt igjen
Razzy wrote:Thanks m8
Stemmer!Vektormannen wrote:Regningen i oppgave D er nok ikke helt riktig, og figuren er ikke helt riktig. Punktet A vil ikke være rett over punktet R dersom du tenker at R ligger på linja mellom B og C. Trekanten ABC står ikke vinkelrett på xy-planet, den er tiltet litt "mot oss" på figuren (vi dreier jo pyramiden mer enn 90 grader!). Men det du vet (og dette var helt riktig tenkt ovenfor) er at z-koordinaten til A er det samme som avstanden fra A og rett ned til planet. ...
Tiltet litt mot oss? Koordinatene til A er jo (0,0,0) og koordinatene til D (0,0,8) - sier ikke dette at disse står ganske så vinkelrett?Vektormannen wrote:Regningen i oppgave D er nok ikke helt riktig, og figuren er ikke helt riktig. Punktet A vil ikke være rett over punktet R dersom du tenker at R ligger på linja mellom B og C. Trekanten ABC står ikke vinkelrett på xy-planet, den er tiltet litt "mot oss" på figuren (vi dreier jo pyramiden mer enn 90 grader!). Men det du vet (og dette var helt riktig tenkt ovenfor) er at z-koordinaten til A er det samme som avstanden fra A og rett ned til planet. Men har du ikke regnet ut denne avstanden tidligere? ...

