matematikk.net

1) Ved de olympiske lekene i Seoul i 1988 løp Ben Johnson 100 meter på 9,83 s. Farten hans (v) i m/s kan beskrives ved funksjonen
v(t) = 12,42 - 0,0944t - 12,42*0,4937^t der t er tiden i sekunder fra start.

a) finn et uttrykk for akselrasjonen a(t). (her prøvde jeg å derivere siden a(t)=v'(t), men fikk ikke riktig svar.)

b) finn et uttrykk for forflytningen s(t). (her skal man vel antiderivere siden v(t)=s'(t).., men gjør noe feil her også)


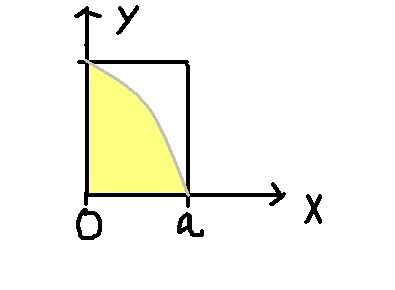
2) Figuren viser grafen til y = a^2 - x^2
vis at arealet av det gule området er 2/3 av rektangelets areal.

Håpløs oppgave.

Han vant, men blei seinere fratatt gullet for å ha spist ulovlige drops.

Han løp på 9.79 s. (Men den gamle rekorden var 9.83 trur jeg.)

Vis oss hva du har gjort, så får du nok hjelp.

det som er problemet er dette leddet: - 12,42*0,4937^t
Både når jeg skal derivere og antiderivere i oppgave 1, gjør jeg feil... Hva skal jeg gjøre med t'en som er opphøyd og hva gjør jeg når det er et gangestykke?

håper noen kan hjelpe!

Hei hopp.
Her kommer et forslag. Håper det er i nærheten hvertfall.

[tex] f(x) = 12,42 \cdot 0,4937^t [/tex]
Denne kan skrives på en annen måte:
[tex] f(x) = 12,42e^{x(ln 0,4937)} [/tex]
Vi deriverer på vanlig måte, og husk at den deriverte av [tex]e^x[/tex] er [tex]e^x[/tex].
Jeg har ingen logaritmekalkulator i nærheten, så du får trykke selv.
[tex] f \prime (x) = 12,42 \cdot ln 0,4937 \cdot e^{x(ln 0,4937)}[/tex]
[tex] f \prime (x) = 12,42 \cdot ln 0,4937 \cdot 0,4937^x[/tex]
Den deriverte av [tex] a^x [/tex] er [tex] ln a \cdot a^x [/tex], husk det.
Faktoren 12,42 ganger vi med ln a og beholder [tex] a^x [/tex] i regnestykket.

Håper ikke jeg har surra nå da..

sett konstanten på utsiden og bruk intergralformelen

[symbol:integral][tex]a^x dx= a^x/ln(a)[/tex]

på oppgave b har jeg nå
s(t) = 12,42t - 0,0472t^2 - 12,42 *(0,4937^t/ln 0,4937)

kanskje et dumt spørsmål, men hvordan skal jeg trekke sammen den siste delen?
svaret skal bli:

s(t) = 12,42t - 0,0472t^2 + 17,60 * 0,4937^t - 17,60

2)
[tex]y=f(x)=a^2\,-\,x^2[/tex]
slik at y(0) = a[sup]2[/sup] og x=a

[tex]A(rektangel) = A_R=x\cdot y=a^3[/tex]

[tex]A_{gul}=\int_0^a y {\rm dx}=\int_0^a (a^2\,-\,x^2) {\rm dx}=[a^2x\,-\,{x^3\over 3}]_0^a[/tex]

[tex]A_{gul}={2\over 3}a^3[/tex]

[tex]\frac{A_{gul}}{A_R}={2\over 3}[/tex]

Janhaa wrote:
[tex]A_{gul}=\int_0^a y {\rm dx}=\int_0^a (a^2\,-\,x^2) {\rm dx}=[a^2x\,-\,{x^3\over 3}]_0^a[/tex]

Tusen takk, men skjønner ikke denne delen av regnestykket..

Skal det ikke egentlig bli 1/3 a^3 når man antideriverer a^2? Og hvorfor har du satt en x bak?

krivol wrote:

Janhaa wrote: [tex]A_{gul}=\int_0^a y {\rm dx}=\int_0^a (a^2\,-\,x^2) {\rm dx}=[a^2x\,-\,{x^3\over 3}]_0^a[/tex]

Tusen takk, men skjønner ikke denne delen av regnestykket..
Skal det ikke egentlig bli 1/3 a^3 når man antideriverer a^2? Og hvorfor har du satt en x bak?

husk at a er en konstant, da gjelder

[symbol:integral]a dx = a*x + C

Deriverer du høyre sia, skal den bli lik integranden (utrykket til høyre for integralet).

(a[sup]2[/sup]x - x[sup]3[/sup]/3) ' = a[sup]2[/sup] - x[sup]2[/sup]

ok, stemmer