matematikk.net

Jeg har begynnt å se på litt kontur integrasjon, samt nytteverdien av dette når man integrerer på den reelle aksen. Prøvde meg med integralet;

[tex]\int_{-\infty}^\infty \frac{e^{itx}}{x^4 + 5x^2 + 4} dx[/tex]

altså å løse det ved å utvide integrasjons konturen til "[tex]\gamma[/tex]" =



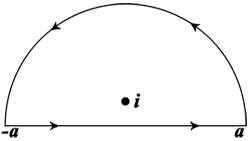
og la a gå til uendelig, inni denne konturen har [tex]f(z)=\frac{e^{itx}}{x^4 + 5x^2 + 4}[/tex] polene i og 2i.

å regne ut "residues" gikk jo fint det;

[tex]\text{Res}(f,i) = \lim_{z\to i} \frac{(z-i)e^{itz}}{z^4 + 5z^2 + 4} = \lim_{z\to i} \frac{e^{itz}}{(z+i)(z-2i)(z+2i)} = \frac{e^{-t}}{6i} = -i\frac{e^{-t}}{6} \\ \text{Res}(f,2i) = \lim_{z\to 2i} \frac{(z-2i)e^{itz}}{z^4 + 5z^2 + 4} = \lim_{z\to i} \frac{e^{itz}}{(z+i)(z-i)(z+2i)} = \frac{e^{-2t}}{-12i} = i \frac{e^{-2t}}{12}[/tex]

så;

[tex]\oint_\gamma \frac{e^{itz}}{z^4+5z^2+4} dz = 2\pi i (i\frac{e^{-2t}}{12} - i\frac{e^{-t}}{6}) = -2\pi (\frac{e^{-2t}-2e^{-t}}{12}) = \frac{\pi}{6}(2e^{-t} - e^{-2t})[/tex]

Men problemet oppstår når jeg skal bruke "the estimation lemma" for å vise at integralet av f(z) over konturen "[tex]\Gamma[/tex]" =



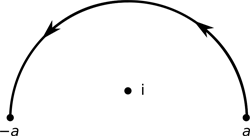
går mot null når a går mot uendelig altså at;

[tex]\lim_{a\to \infty} \oint _\Gamma \frac{e^{itz}}{z^4+5z^2+4} dz = 0[/tex]

Dette på slutten her er altså problemet mitt hvis hva jeg faktisk spørr om her er vanskelig å finne

edit: her er wikipedia linken til estimation lemma http://en.wikipedia.org/wiki/Estimation_lemma

jeg forstår det om lengden til konturen, men har problemer med det andre.

Generelt gjelder det for et komplekst polynom P av grad n at det fins en konstant c så [tex]|P(z)|\le c|z|^n[/tex] når |z| er tilstrekkelig stor. Dette heter Liouvilles teorem og er ikke så fryktelig vanskelig å vise såvidt jeg husker.

tror jeg skjønner taktikken ja, å vise det for 1/(c|z|^n) hadde nok blitt lettere. men dukker det ikke opp et problem e^{itx} i telleren?

forresten, fant et lemma nå som jeg synes passer til situasjonen:

http://mathworld.wolfram.com/JordansLemma.html

dette var egentlig ganske logisk, vise at grensverdien til uendelig blir null over nettop en slik halvsirkel.

det er jo lettforståelig at [tex]\lim_{R \to \infty} \frac{1}{R^4e^{5i\theta} + 5R^2e^{2i\theta} + 4} = 0[/tex] for [tex]\theta[/tex] mellom 0 og [tex]\pi[/tex]

også telleren blir enkel [tex]\lim_{R \to \infty} e^{tiRe^{i\theta}} = \lim_{R \to \infty} e^{tiR(i\sin(\theta)+\cos(\theta))} \\ = \lim_{R \to \infty} e^{tR(i\cos(\theta)-sin(\theta))} = \lim_{R\to \infty} e^{tRi\cos(\theta)} \cdot e^{-tR\sin(\theta)}[/tex]

som klart går mot null.

men bare hvis t>0, (den siste delen av den siste grenseverdien).

for å utvide funksjonen til negative t, hva kan jeg gjøre?

Jeg har ikke lest dette så nøye, men er problemet ditt å vise at grenseverdien når a->inf av integralet langs halvsirkelen blir 0? I så fall er det vel ML-ulikheten.

ja, ML ulikheten var det originale spørsmålet, men så synes jeg jordans lemma var ganske fin den òg?

det blir jo basically den sammen tingen, men jeg synes jordans lemma var mer lettforståelig.