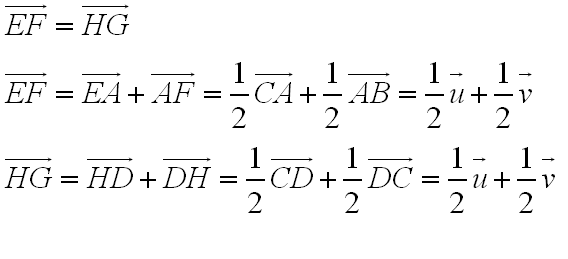matematikk.net

Heihei,

Har litt problemer med å skjønne hvordan denne skal gjøres:

Tegn en vilkårlig firkant ABCD. Kall midtpunktet på sidene for E, F, G og H. Bruk vektorregning til å vise at firkanten er et parallellogram.

Se figuren (trykk på den for å se et større bilde):



Prøv å vise at:

[tex]\vec {EF} = \vec {HG} [/tex]

Da må nødvendigvis også:

[tex]\vec {FG} = \vec {EH} [/tex]

Dermed er firkant EFGH et parallellogram.

EDIT: La inn en bedre figur.

Fikk ikke TEX til å virke, så tok bilde i stedet.

Har jeg bevist at EF = HG under, eller er jeg helt på bærtur?

Forresten, tegnet ikke den samme firkanten som deg, men er dette riktig fremgangsmåte?

Litt kronglete bevis, kanskje noen andre har et mer elegant bevis? Be my guest!

Ok. Vi starter med å uttrykke de to vektorene [tex]\vec {EF}[/tex] og [tex]\vec {HG}[/tex] ved hjelp av vektorer i firkant [tex]ABCD[/tex]


1)

[tex]\vec {EF} = \vec {EB} + \vec {BE} = \frac12 \vec {AB} + \frac12 \vec {BC}[/tex]

2)

[tex]\vec {HG} = \vec {HD} + \vec {DG}[/tex]

Regner videre på denne vektoren:

[tex]\vec {HG} = \frac12 \vec {AD} + \frac12 \vec {DC} [/tex]

[tex]\vec {HG}= \frac12 (\vec{AB} + \vec{BC} + \vec{CD}) + \frac12 (\vec{DA} + \vec{AB} + \vec{BC}) [/tex]

[tex]\vec {HG} = (\vec {AB} +\vec {BC}) + \frac12 \vec{DA} + \frac12 \vec{CD}[/tex]

[tex]\vec {HG}= 2 \cdot \vec {EF} - (\frac12 \vec {AD} + \frac12 \vec {DC})[/tex]

[tex]\vec {HG} = 2 \cdot \vec {EF} - \vec {HG}[/tex]

[tex]2 \cdot \vec {HG} = 2 \cdot \vec {EF}[/tex]

[tex]\vec {HG} = \vec {EF}[/tex]

Siden punktene[tex] EFGH[/tex] danner en firkant følger det at da må også:

[tex]\vec {FG} = \vec {EH}[/tex]

Dermed har vi bevist at firkant [tex]EFGH[/tex] er et parallellogram.

Snowreven: Var dette greit eller? Kunne vært greit med en tilbakemelding, jeg brukte tross alt en del tid på denne oppgaven! Eller var det helt bortkastet arbeid av meg?

enig, var litt kronglete den der , hva med denne?


[tex]\vec {EF} = \frac12 ( \vec {AB} + \vec {BC} ) = \frac12 \vec {AC}[/tex]

[tex]\vec {HG} = \frac12 ( \vec {AD} + \vec {DC} ) = \frac12 \vec {AC}[/tex]

[tex] EFGH [/tex] er et parallellogram fordi [tex] \vec {EF} = \vec {HG}[/tex]

ettam wrote:Snowreven: Var dette greit eller? Kunne vært greit med en tilbakemelding, jeg brukte tross alt en del tid på denne oppgaven! Eller var det helt bortkastet arbeid av meg?

lagde meg konto kun for å takke dere for hjelpen med å forstå problemet.
siden Snowreven ikke ga noe takk, så gjør jeg det håper på et fint samarbeid skulle jeg stå fast i matematikken min