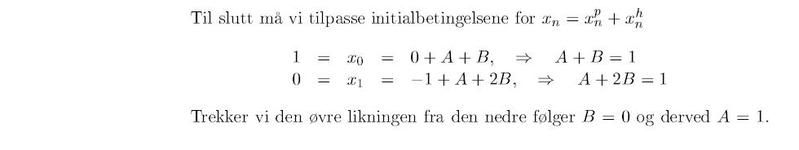matematikk.net

Hei, i en eksamen oppgavene så skal vi finne den første deriverte, andre deriverte og tredje deriverte til funksjonen f(x) = (1+x)^1/2. Jeg vet hvordan man finner første deriverte, men resten er helt blank.

Kunne noen være så snill å hjelpe meg.

Tusen takk på forhånd, = ).

mvh
Fderivert

Er jo bare å bruke produktregelen, kvotientregelen og kjerneregelen på den første og andre deriverte av funksjonen. Du kjenner til disse?

jaja, har brukt det, men fikk andre svar enn fasit. Den første deriverte er jo 1/2(1+x)^1/2, men da for å finne andre deriverte er å gjøre det samme med første deriverte, men her må kovitient regelen brukes. Jeg brukte den, men det ble noe rare greier.

Svaret for den andre deriverte er: -(1+x)^-3/2 /4.

Men hvordan har de kommet frem til akkurat dette!!?

mvh
Fderivert.

[tex]f(x)=(x+1)^{\frac{1}{2}} \Rightarrow f(x)=\sqrt{x+1}[/tex]

Og kjent er den derivert av [tex]\sqrt{x} = \frac{1}{2\sqrt{x}}[/tex]

Så da blir det:

[tex]f(x)^,=\frac{1}{2\sqrt{x+1}[/tex]

[tex]f(x) = (1+x)^{\frac{1}{2}} \\ f \prime (x) = \frac12(1+x)^{-\frac12} \\ f \prime \prime (x) = -\frac12 \cdot \frac12 (1+x)^{-\frac32} = -\frac14 (1+x)^{-\frac32} = \frac{-(1+x)^{-\frac32}}{4}[/tex]

Aha, Takk Realist1. Man må ta den ned igjen, men med skiftet fortegn. også må huske -1 hver gang. Tusen takk, nå har ting klarnet for meg, yey. You tha man.

Takker andre også for den hjelpen de gav.


mvh
Fderivert

Hei har et annet spørsmål. Dette dreier seg om en differensligning.

Det jeg engentlig lurer på her er hvordan de har brukt de startverdiene og satt opp den ligningen de har satt opp?? (se bilde ved grønn strek).

Bilde:

De har bare satt inn n=0 og n=1 i den generelle løsningen rett over for å finne konstantene C og D.

Aha, hehe nå skjønner jeg det. Tusen takk for hjelpen. = ).

Nå har jeg truffet en liten vegg igjen. Det jeg lurer på er hvorfor B=0 og A=1, burde det ikke være omvendt??



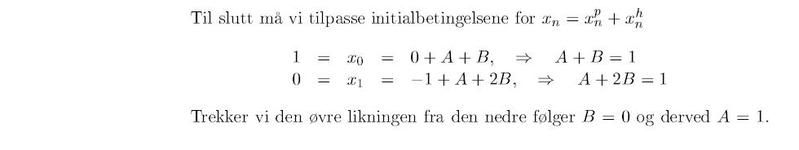
mvh
Fderivert

Det blir riktig med B=0 og A=1. Det kan du se på flere måter. Foreksempel slik som det står. Da blir det:

[tex]\text{ }A+2B=1[/tex]
[tex]-(A+B=1)[/tex]
[tex]=0+B=0[/tex]

som gir B=0 og setter du det inn i en av de andre ligningene får du A=1.

Eller du kan bruke innsettingsmetoden. Det blir

[tex]A=1-B[/tex] finner et uttrykk for A

[tex](1-B)+2B=1[/tex]
[tex]1+B=1[/tex]
[tex]B=0[/tex]

setter det inn i andre ligningen og får A=1

ellers kan du bare se det ved å se på ligningene.

1-A er både lik B og 2B derfor kan B kunne være null.

Å ja, hehe takk. Tusen takk. Nå skjønner jeg hvordan det funker.
You tha man

mvh
Fderivert

Hei, har eksamen snart, og sitter fast på en oppgave. Føler at jeg kan diff ligninger, men denne skjønner jeg bare ikke hvorfor det blir akkurat det svaret:




mvh
Fderivert

Utnytt informasjonen du har fått, hva vil det si at y(x)=sin x er ei løsning? Sagt på en annen måte, hvis f(x)=y''(x)-2*y(x) og y(x)=sin x, er f(x) lik?

å ja, okok takk. Var lettere måten du skrev det på. Da blir svaret -3sinx.

Har et annet lite spørsmål: den deriverte til xtanx er 1/cos^2x, men hva er den andre deriverte. Hvordan er reglene, er det produktregelen? Har prøvd den men, får -2sinx/cos^4x, og det trur jeg er feil!!


mvh
Fderivert