matematikk.net

Hei!

Hvis man har 2 likninger, fx:

2x + 3y = 5
x + 4y = 4

så blir koeffisientmatrisen [2 3] .. og da blir det veldig naturlig for meg å
..........................................[1 4]
se på vektorene i matrisen som [2 3] og [1 4]. Men idag leste jeg litt om lineære kombinasjoner, og der ble x'ene og y'ene satt utenfor, sånn her:

x[2] og y[3]. Så langt alt vel. Men kolonnene ble snakket om som
..[1].......[4]

vektorer - hvor mange av kolonne 1 og kolonne 2 skal man ta for å komme fram til løsningsvektoren. De ble også snakket om geometrisk - vi beveger oss 2 bortover og 1 oppover, etc. Hvordan kan det gå ann, når både 2 og 1 er x-komponenter? Det forvirrer meg så ekstremt.. hvordan kan vektorene bestå av 2 x-komponenter og 2 y-komponenter? Jeg ville jo tro at alle vektorer ikke kan ha mer enn 1 av hver komponent. Når jeg bare ser på det som en matrise, skjønner jeg systemet og poenget, men intuitivt gir det ingen mening for meg.

Takk på forhånd hvis noen kan hjelpe meg ut av suppa!

Ps. sorry for litt rotete post, vet ikke hvordan jeg skal skrive matriser her :P

2 og 1 er ikke x-komponenter. Tenk på ligningssystemet på følgende måte:

Du har to vektorer i planet, (2,1) og (3,4). Problemet er å finne en lineærkombinasjon av disse to som blir vektoren (5,4). Mao. finn skalarer x og y slik at (2,1)x+(3,4)y=(5,4)

Skjønner?

Takk så mye for hjelpa! Jo, skjønner litt mere nå. Men det med når x og y er skalarer eller ikke forvirrer meg litt fortsatt.. for eksempel en rotasjonsmatrise:



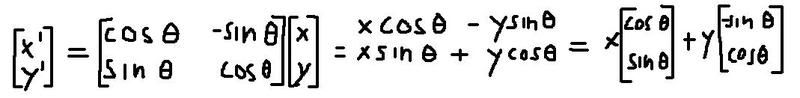
Her består jo den første [x y] kolonnevektoren av x og y komponenter, det er ikke skalarer right? For man putter inn et (x,y) punkt/vektor og får ut det roterte punktet. Hvordan blir det da med den siste fremstillinga der som en lineær kombinasjon, hvordan kan jeg gå over fra å tolke x og y som vektorer til skalarer?

Sorry om det her er veldig dumme/basic spørsmål - sitter og prøver å lære meg det sjøl, men syns ikke det er så lett å få intuisjonen bak det :P Takk igjen!

Situasjonen her er jo litt annerledes siden det ikke lenger er en ligning, men en transformasjon. Du har gitt vektoren (x,y) og rotasjonsmatrisen, og finner dermed den nye vektoren (x',y') fra uttrykket ditt.


Jeg skjønner ikke helt hva du er ute etter. Å skrive om et sett med ligninger på matriseform er ikke noe hokus pokus. Det er bare en lettvint og kompakt måte å uttrykke noe på. Du bør ikke fokusere for mye på å finne en eller annen geometrisk tolkning på kolonne eller radvektorene. Det er bare ord man benytter. Råd: Fokuser heller på å lære teknikkene for å løse slike ligningssett med matriser.

Jo, sant det, dårlig av meg.. Det som er, jeg har lest en del lineær algebra, og kan mye basic shit, men jeg føler at jeg mangler litt grunnleggende forståelse(som må sitte hvis jeg skal komme meg videre) når jeg blir forvirra av tolkinga av noe så simpelt som rad/kolonnevektorer.

Har man likninga 2x + 3y = 5, er det jo snakk om å finne et tall i x og y-retning som tilfredsstiller likninga, men hvis man tar en likning til og skriver om til matriseform, så blir x'ene og y'ene skalarer, og det som før var x-ledd blir til en vektor i planet. Er det ungdomskolematte å se på likninga over som en linje i planet, og bedre å se på x'ene og y'ene som bare skalarer, eller hva?

Det kommer vel tilbake til det første eksempelet du forklarte til meg - det er sånn folka på MIT(de har noen lectures på youtube som jeg ser på) ser på det, men jeg har ikke kommet over slik tolkning i andre lærebøker, der er radene vektorer og kolonnene andre likninger så og si. Vet ikke om jeg forklarte problemet mitt noe bedre nå men, håper det! Setter veldig pris på hjelpa :)

For det første; lineær algebra kan være komplisert så ikke bebreid deg selv for at noe av det grunnleggende er vanskelig å få god intuisjon på.

Radvektorenes tolkning: Eks. 2x+3y=5. (2,3)*(x,y)=5. (* skalarprodukt)

Én lineær ligning med én ukjent har et punkt som løsning, én ligning med to ukjente har en linje i R^2, én ligning med tre ukjente har et plan i R^3 etc.

n ligninger med to ukjente har snittet av n linjer i R^2 som løsning, etc.

n ligninger med tre ukjente har snittet av n plan i R^3 som løsning, etc.

Aha! Sånn hadde jeg enkli ikke tenkt på matriser før(av en eller anna grunn), selvom jeg ser ligningssystemer sånn ^^ Kongefett, tusen takk!