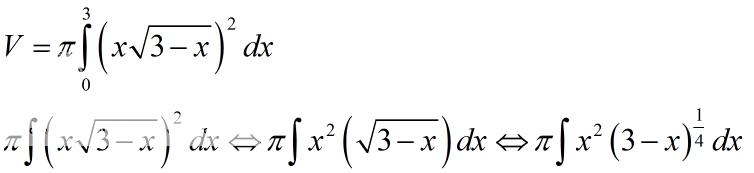matematikk.net

Måtte poste som image, fikk ikke til å skrive [tex]$${3^{{1 \over 4}}}$$[/tex] som kvadratrot tegn i TexKoder...

Uansett, hva gjør jeg med dette integralet? Forsøkte å gå løs på det med delvis integrasjon, men mistenker at jeg har tatt en spansk en et eller annet sted i omgjøringen.

Hva sier dere?

DU må også opphøye [tex]{\sqrt {3-x}}^2[/tex] i tillegg til at du får x^2, og så blir det nok litt lettere. (Hva er kvadratroten av noe opphøyd i annen, SVAR: det som står under kvadratroten )

mstud wrote:DU må også opphøye [tex]{\sqrt {3-x}}^2[/tex] i tillegg til at du får x^2, og så blir det nok litt lettere. (Hva er kvadratroten av noe opphøyd i annen, SVAR: det som står under kvadratroten )

Så sant så sant! Nå skal den løses!

[tex]$$\pi {\int\limits_0^3 {\left( {x\sqrt {3 - x} } \right)} ^2}dx \Leftrightarrow \pi \int\limits_0^3 {{x^2}{{\left( {\sqrt {3 - x} } \right)}^2}} dx \Leftrightarrow \pi \int\limits_0^3 {{x^2}\left( {3 - x} \right)dx} $$[/tex]

Vi har omskrevet uttrykket til noe vi kan bruke delvis integrasjonsmetode på

[tex]$$\pi \left( {\int {{x^2}\left( {3 - x} \right)dx} } \right) = \pi \left( {{1 \over 3}{x^3}\left( {3 - x} \right) - \int {{1 \over 3}{x^3}\left( { - 1} \right)dx} } \right)$$[/tex]

Vi bruker delvis integrasjon for å finne det ubestemte integralet

[tex]$$\pi \left( {{x^3} - {1 \over 3}{x^4} + {1 \over 3}\int {{x^3}dx} } \right)$$[/tex]

[tex]$$\pi \left( {{x^3} - {1 \over 3}{x^4} + {1 \over 3}*{1 \over 4}{x^4}} \right) + C$$[/tex]

[tex]$$\pi \left( {{x^3} - {1 \over 3}{x^4} + {1 \over {12}}{x^4}} \right) + C$$[/tex]

[tex]$$\pi {x^3} - {1 \over 4}\pi {x^4} + C$$[/tex]

[tex]$$\left[ {\pi {x^3} - {1 \over 4}\pi {x^4}} \right]_0^3 = \left( {\pi *{3^3} - {1 \over 4}\pi *{3^4}} \right) - \left( {\pi *{0^3} - {1 \over 4}\pi *{0^4}} \right) = {{27} \over 4}\pi $$[/tex]

Vi setter inn integrasjonsgrensene og får svaret som stemmer med fasit og kalkulatorsvaret.