matematikk.net

Oppgaven:
[tex]$$y = 2\sqrt x + \tan \left( {3x} \right)$$[/tex]


Mitt løsningsforslag:
[tex]$$y^\prime = 2 \cdot {1 \over 2}{x^{ - {1 \over 2}}} + \left( {1 + {{\left( {\tan 3x} \right)}^2}} \right) \cdot 3$$[/tex]

[tex]$$y^\prime = \underline {{{3\left( {1 + {{\left( {\tan 3x} \right)}^2}} \right)} \over {\sqrt x }}} $$[/tex]


Kalkulatoren forteller meg at dette er feil:



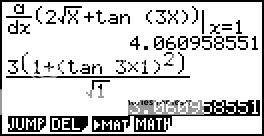Wolfram svarer med dette:


1. Ser dere feilen min?
2. Hva betyr det når Wolfram skriver [tex]$${\sec ^2}$$[/tex]?

På forhånd takk

Er oppgaven [tex] y \, = \, 2\sqrt{x} + \tan(3x)[/tex] ?

Fordi da har du antakeligvis trykket inn feil på wolfram alpha...

Får uansett det samme som deg når jeg deriverer, tror kanskje forskjellen er grader og radianer =)

Nebuchadnezzar wrote:Er oppgaven [tex] y \, = \, 2\sqrt{x} + \tan(3x)[/tex] ?

Fordi da har du antakeligvis trykket inn feil på wolfram alpha...

Får uansett det samme som deg når jeg deriverer, tror kanskje forskjellen er grader og radianer =)

Ja oppgaven er: [tex]$$y = 2\sqrt x + \tan \left( {3x} \right)$$[/tex]

Som du ser fikk jeg fortsatt feil når jeg stilte på til grader istede for radianer.

Jeg kan heller ikke se jeg har tastet feil på Wolfram.

hm...

[tex] \frac{d}{{dx}}f\left( x \right) = \frac{1}{{\sqrt x }} + \left( {1 + \tan {{\left( {3x} \right)}^2}} \right)3 [/tex]

[tex] \frac{d}{{dx}}f\left( x \right) = \frac{{1 + 3\sqrt x \left( {1 + \tan {{\left( {3x} \right)}^2}} \right)}}{{\sqrt x }} [/tex]

Og i wolfram har du skrevet gangetegn, når du skulle ha skrevet et plusstegn =)

[tex]1 + \tan {\left( a x \right)^2} = 1 + \frac{{\cos {{\left( a x \right)}^2}}}{{\sin {{\left( a x \right)}^2}}} = \frac{{\sin {{\left( a x \right)}^2} + \cos {{\left( a x \right)}^2}}}{{\sin {{\left( a x \right)}^2}}} = \frac{1}{{\sin {{\left( a x \right)}^2}}} = \sec {\left( a x \right)^2}[/tex]

Nebuchadnezzar wrote:[tex] \frac{d}{{dx}}f\left( x \right) = \frac{1}{{\sqrt x }} + \left( {1 + \tan {{\left( {3x} \right)}^2}} \right)3 [/tex]

[tex] \frac{d}{{dx}}f\left( x \right) = \frac{{1 + 3\sqrt x \left( {1 + \tan {{\left( {3x} \right)}^2}} \right)}}{{\sqrt x }} [/tex]

Og i wolfram har du skrevet gangetegn, når du skulle ha skrevet et plusstegn =)

[tex]1 + \tan {\left( a x \right)^2} = 1 + \frac{{\cos {{\left( a x \right)}^2}}}{{\sin {{\left( a x \right)}^2}}} = \frac{{\sin {{\left( a x \right)}^2} + \cos {{\left( a x \right)}^2}}}{{\sin {{\left( a x \right)}^2}}} = \frac{1}{{\sin {{\left( a x \right)}^2}}} = \sec {\left( a x \right)^2}[/tex]

Aha! Tusen hjertelig Nebu, jeg får ta meg en pause fra matten, man ser tydeligvis ting litt i kryss når man sitter for lenge

Fortsatt god kveld