matematikk.net

Er det berre fasiten som er upresis, eller finst det ein meir presis måte å rekne ut dette på?

Frå 2MX, Erstad:
Eg har nettopp lært at 1/2sinC*a*b = arealet av ▲ ABC

2.2
Ei tomt har form som ein firkant ABCD. Finn arealet av tomta når
a) ∠ A = 90°, AB = 24 m, AD = 16 m, BC = 22 m og ∠ CBD = 63°


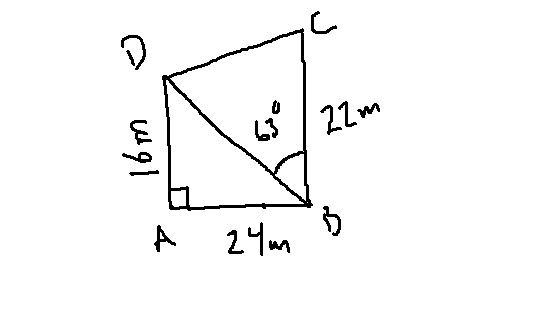
Arealet av ▲ ABD:
(16m * 24m)/2 = 192 m^2

Lengda av BD:
24^2 + 16^2 = x^2
832^2 = x^2
[symbol:rot] 832 = [symbol:rot] x
x = 28.8

BD = 28.8 m

Arealet av ▲ BCD:
1/2sin(63)*28.8*22 = 282 m^2

Arealet av ▲ ABD + ▲ BCD = ABCD
192 m^2 + 282 m^2 = 474 m^2

Fasit = 470 m^2

Alle tallene i din oppgave er oppgitt med to siffer. Dermed skal også svaret ditt oppgis med en nøyaktighet på to siffer.

Gjeldende siffer.

Gjeldande siffer var stikkordet, ja. Det blei repetert litt seinare i boka, og er jo forståeleg nok, men ikkje heilt opplagd om ein ikkje har holdt på med matte ei stund... Takk for tipset, begge to!

OK, eg slit litt med dette enno.

Aschehoug R1, oppgåve 1.41.

Finn vinklane i trekanten ABC
a)
A = (2, 3), B = (6, 4) og C = (4, 5)

Eg byrjar med vinkel A:
[tex]\vec{AB}=[6-2, 4-3] = [4, 1][/tex]
[tex]|\vec{AB}|=\sqrt{4^2 + 1^2}= \sqrt{17}[/tex]

[tex]\vec{AC}=[4-2,5-3]=[2,2][/tex]
[tex]|\vec{AC}|=\sqrt{2^2+2^2}=\sqrt{8}[/tex]

Så brukar eg skalarproduktet for å finne vinkelen. For å unngå heile problemet med å velge desimalar, brukar eg kvadratrota vidare.

[tex]cosA=\frac{[4,1]*[2,2]}{\sqrt{17}*\sqrt{8}}[/tex]

[tex]A = \arccos{\frac{10}{\sqrt{17}*\sqrt{8}}}[/tex]

Kalkulatoren gjev meg 30,963756 ... Boka gjev 31,0.

Pga. eg ikkje har rekna ut kvadratrøtene i mellomrekningane, har eg ikkje noko klar formeining av kor mange gjeldande siffer eg skal bruke. Det enklaste hadde kanskje vore ingen desimalar - 31, alternativt 31,0 eller 30,964. Kvifor brukar dei akkurat ein desimal?

Eller er det implisitt at ein skal rekne ut kvadratrøtene i mellomrekningane med to desimalar - altså [symbol:rot]8 = 2,82 og [symbol:rot]17 = 4,12 - altså tre gjeldande siffer, og derfor brukar dei også tre gjeldande siffer i svaret?

Ved første løysingsforsøk "tulla" eg tydelegvis - eg brukte 4,1 for [symbol:rot]17, og 2,8 for [symbol:rot]8. Dette resulterte i at A blei 29,4156 ..., som eg skreiv som 29 gradar.

Er veldig takksam om nokon steg for steg kan forklare korleis ein tenker angåande desimalar/gjeldande siffer i denne delen av oppgåva - gjer ein feil her, så forplantar det seg jo naturleg nok vidare

Riktige burde vært 31 blank. Fysikkbøkene er nøyere med dette, mens mattebøkene gjerne slurver litt mer. Og det kommer litt ann på situasjonen.

Selv fikk jeg trekk for å oppgi alle svarene mine med 20 desimalers nøyaktighet på videregående.

Så lenge du har et riktig svar, så ikke bry deg så nøye om hvor mange desimaler matteboken din bruker.

Bare hold deg til at svaret ditt skal inneholde like mange desimaler, som det tallet i oppgaven med færrest desimaler.