matematikk.net

Anta at linjen y = 5 x − 4 er tangent til kurven y = f(x) der x = 3. Newtons metode skal brukes til å finne en rot til likningen f(x) = 0 med første tilnærming x[sub]1[/sub] = 3. Finn andre tilnærming x[sub]2[/sub].

Jeg kommer ikke i gang med denne oppgaven. Lærerens forklaring av Newtons metode gikk litt for kjapt, og mange medelever spøker om akkurat dette fordi læreren vår har doktorgrad i matte. Sannsynligvis synes han det går for tregt selv

Har en liten håndfull med slike oppgaver som nevnt ovenfor, bare med andre likninger andre x[sub]n[/sub], så hadde satt pris på litt dytt.

Prinsippet i Newtons metode er at du starter i et start punkt (her x = 3). Så går du direkte opp/ned i y-retning til du treffer funksjonen. Så føler du tangenten i punktet ned til der den treffer x-aksen. Dette blir da det neste punktet. Prosessen gjentas så helt til man ser at følgen av x-verdier konvergerer, og man oppnår den nøyaktigheten man ønsker. En illustrasjon:



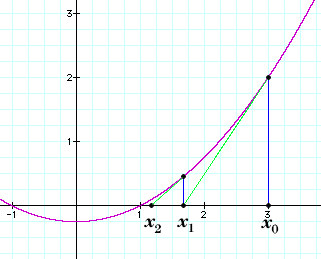
(På denne figuren er første tilnærming x_0, men i ditt tilfelle x_1, bare så det ikke virker forvirrende.)

Her har du oppgitt tangentlinjen, så da er vel saken grei?

Ok, så man følger tangenten til x-aksen, finner x-verdien der.

Deretter finner man punktet (x, f(x)) til den x-verdien man fant i linja over, tangenten i dette punktet, og på nytt ned til x-aksen. Rinse and repeat.

Er det slik?

Ja, det stemmer.

Men hvordan finner man tangenten i det nye punktet når man ikke vet funksjonsuttrykket?

Ok, disregard det siste der, jeg fant ut av det.

Har løst en liten drøss med oppgaver nå, vha Newtons metode, men satt meg fast på en ny en.

Bruk Newtons metode til å finne den positive roten til likningen sin x = x[sup]2[/sup] med en nøyaktighet på 6 desimaler.

Jeg prøver å gjøre om til sinx-x[sup]2[/sup]=0, men er usikker på hva jeg skal gjøre herfra. Skal jeg velge en vilkårlig x å starte med? Virker som at uansett hva jeg velger, så blir det verdier som er ganske kjipe å jobbe videre med.

Bruk middelverdi setningen og vis at

[tex]sin(x) = x^2[/tex] har en rot på intervallet [tex]x\in[0,1][/tex]

Som for eksempel gir at [tex]x_n = 1[/tex] er en god initialverdi

Lurt å lage en grov skisse av de to funksjonene først. Dersom du velger x=0 vil jo Newtons metode konvergere umiddelbart, så det er en ulur initalverdi.

Definer funksjonen [tex]f(x)=sin(x)-x^2[/tex]. Problemet er nå omformet til å finne det positive (x>0) nullpunktet til f(x). Den eneste tekniske finurligheten i slike oppgaver er å finne en passende startverdi, og der kommer skissen inn i bildet. Velg en startverdi [tex]x_0[/tex] som ligger så nært som mulig det punktet (x-verdien) der funksjonene [tex]\sin(x)[/tex] og [tex]x^2[/tex] krysser hverandre på skissen.

EDIT: Fikk det til, hehe. Takk for hjelpa!