matematikk.net

Dette er oppgaven slik jeg har fått den:



Her er mitt forsøk på løsning:



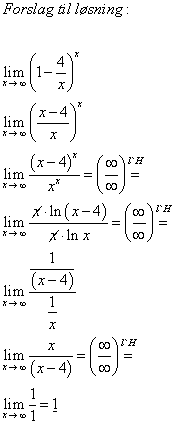
Og hva er så deres kommentar? hehe

Litt usikker på om du har derivert riktig. Men jeg ville heller omdefinert grensen, siden vi ved første innfall får 1[sup] [symbol:uendelig] [/sup]

Kan skrive om til [tex]\lim_{e^x \to \infty} \ xln(1-\frac{4}{x})[/tex]

Og etter det sette inn u=1/x.

Nå er ikke jeg noen jævel på grenser heller, så er spent på å se utfallet, hehe.

Hint: Bruk den kjende grenseverdien
[tex]e^x = \lim_{n\to \infty} (1+\frac{x}{n})^n[/tex]

Tipset i oppgåva er forresten feil; [tex]e\neq \lim_{n\to \infty}(1-\frac{1}{n})^n[/tex]

Razzy wrote:Dette er oppgaven slik jeg har fått den:



Her er mitt forsøk på løsning:



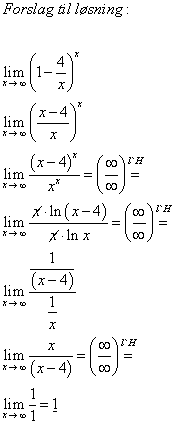
Og hva er så deres kommentar? hehe

Du deriverer feil 1. gang, tror jeg, men er ikke sikker siden jeg ikke kan se hvilke trinn du har gjort

[tex]\lim_{x \rightarrow \infty} \frac {(x-4)^x}{x^x}=\lim_{x \rightarrow \infty} \left( \frac {(x-4)^x}{x^x} \right) ^,[/tex]

Her ser du den deriverte av x^x. [tex](x^x )^, = x^x \cdot (1+ ln(x))[/tex]

Og [tex]((x-4)^x)^,=(x-4)^{x} \cdot ln(x-4)[/tex], hvis ikke jeg husker feil ...

Er det disse du har brukt sammen med brøkregelen:
[tex](\frac {u}{v} )^, =\frac {u^, \cdot v-u \cdot v^, }{v^2}[/tex]

Jeg bare spør for å forsikre oss om at det ikke ligger i derivasjonen

(OT:Du er begynt på bygging. på HiB, ser jeg ...)

Men tror ikke derivasjon på det opprinnelige uttrykket er enkleste måte å finne grenseverdien på...

[tex]y = \lim_{x \to \infty} \left( 1 - \frac{4}{x} \right)^{x} [/tex]

[tex]\ln y = \lim_{x \to \infty} x \ln \left( 1 - \frac{4}{x} \right)[/tex]

[tex]n = \frac{1}{x}[/tex]

[tex]\ln y = \lim_{n \to 0} \frac{\ln \left( 1 - 4n \right)}{n} \qquad \left[ \frac{0}{0} \right] [/tex]

[tex]\ln y = \lim_{n \to 0} \frac{-4}{1-4n}[/tex]

[tex]\ln y = -4[/tex]

[tex] y = e^{-4}[/tex]

Nebuchadnezzar wrote:1. [tex]y = \lim_{x \to \infty} \left( 1 - \frac{4}{x} \right)^{x} [/tex]

2. [tex]\ln y = \lim_{x \to \infty} x \ln \left( 1 - \frac{4}{x} \right)[/tex]

3. [tex]n = \frac{1}{x}[/tex]

4. [tex]\ln y = \lim_{n \to 0} \frac{\ln \left( 1 - 4n \right)}{n} \qquad \left[ \frac{0}{0} \right] [/tex]

5. [tex]\ln y = \lim_{n \to 0} \frac{-4}{1-4n}[/tex]

6. [tex]\ln y = -4[/tex]

7. [tex] y = e^{-4}[/tex]

Hei igjen Nebu, og tusen takk for tilbakemeldingen. Kunne du forklart hva du gjør på linje 3,4 og 5?

Dette forstår jeg (dvs jeg tror jeg forstår):

3. Du innfører en bokstav n fordi du ønsker å ha det på en brøk og benytte l`Hopitalsregel.

4. Du sjekker at l`Hopitalsregel kan brukes, og det kan du fordi teller og nevner går mor null og teller og nevner er deriverbare. Hva har skjedd med uendelighetstegnet? hm har Nebu slurva? Det har nok ikke skjedd nei...

5. Du har nå derivert, vel og merke kun høyre side.

Leser videre i boka i håp om lignende oppgaver

Liker gjerne å bare skrive regningen uten forklaringer, og la personen jeg hjelper tenke litt selv. Som du har gjort. Flott!

På linje 3 så bytter vi ut [tex]\frac{1}{x}[/tex] med [tex]n[/tex]. Som er et lite knep, slik l`hoptial kan benyttes.

Vi ser at vi har [tex]n=\frac{1}{x}[/tex] vi ser at det at x går mot uendelig så går n mot null. Eventuelt

[tex]\lim_{x \to \infty} [/tex]

[tex] \lim_{\frac{1}{n} \to \infty} [/tex]

[tex] \lim_{n \to 0} [/tex]

Også sjekker jeg bare at den er på riktig form og deriverer ja. Det er kun grensen jeg deriverer. Fordi det er kun den som er en grense. Høyreside har ingenting med venstre side å gjøre, mtp deriveringen.

Men du, prøv å bruke definisjonen av den deriverte til å finne den deriverte av [tex]\ln(x)[/tex]

Da får du bruk for litt av snadderet ovenfor

Nebuchadnezzar wrote:Liker gjerne å bare skrive regningen uten forklaringer, og la personen jeg hjelper tenke litt selv. Som du har gjort. Flott!

På linje 3 så bytter vi ut [tex]\frac{1}{x}[/tex] med [tex]n[/tex]. Som er et lite knep, slik l`hoptial kan benyttes.

Vi ser at vi har [tex]n=\frac{1}{x}[/tex] vi ser at det at x går mot uendelig så går n mot null. Eventuelt

[tex]\lim_{x \to \infty} [/tex]

[tex] \lim_{\frac{1}{n} \to \infty} [/tex]

[tex] \lim_{n \to 0} [/tex]

Også sjekker jeg bare at den er på riktig form og deriverer ja. Det er kun grensen jeg deriverer. Fordi det er kun den som er en grense. Høyreside har ingenting med venstre side å gjøre, mtp deriveringen.

Men du, prøv å bruke definisjonen av den deriverte til å finne den deriverte av [tex]\ln(x)[/tex]

Da får du bruk for litt av snadderet ovenfor

Nabu, dette var gøy! Føles nesten ut som du "leker" litt mer hjernen min her. Men skjønner nå hvordan du har kommet frem til denne utregningen - dette vil jeg teste på mer! Du og alle de knepene dine. Er så glad for at du er villig til å vise andre det også.

Hele oppgaven ble jo ganske grei nå egentlig.

Ser på definisjonen til den deriverte nå. Mvh razzy

Tror Razzy er inne på noe. Nebu er flink i matte fordi han bruker skitne triks og knep!

Aleks855 wrote:Tror Razzy er inne på noe. Nebu er flink i matte fordi han bruker skitne triks og knep!

hehe, du kaller det skitne triks. Men det er morro å kunne noen skitne triks! Merker det er endel som skal ha det til at de er veeldig flinke i matte, da er det artig å gi dem noe å tygge på. Finner de det ut med en gang, later jeg bare som at jeg alltid har kunnet det

Å være flik i matte kan bety så mye forskjellig

Du er en røver i hoderegning

Du er en kløpper til å regne ut logiske gåter

Du er en maskin når det kommer til bevisføring

Du er kongen når det kommer til algegebra manipulasjon

Eller du bare kan være en rakker til å bruke skitne triks, du har sett før/ kombinere skitne triks til nye skitnere triks.

Nebuchadnezzar wrote:Å være flik i matte kan bety så mye forskjellig
Du er en røver i hoderegning
Du er en kløpper til å regne ut logiske gåter
Du er en maskin når det kommer til bevisføring
Du er kongen når det kommer til algegebra manipulasjon
Eller du bare kan være en rakker til å bruke skitne triks, du har sett før/ kombinere skitne triks til nye skitnere triks.