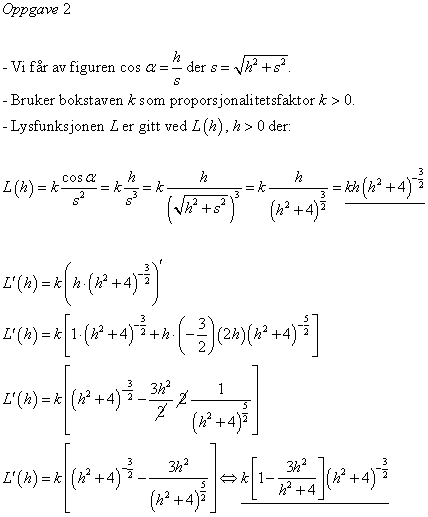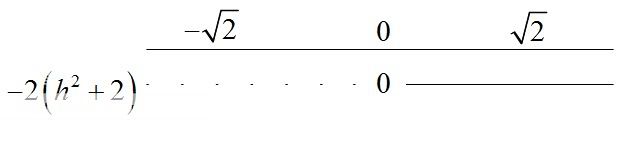Drøfte x-verdi - fortegnslinje
Posted: 12/10-2011 22:17
Hepp hepp!
Her er min deriverte:
[tex]$${k\left[ {1 - {{3{h^2}} \over {{h^2} + 4}}} \right]{{\left( {{h^2} + 4} \right)}^{ - {3 \over 2}}}}$$[/tex]
Den har nullpunktet [tex]$${+\sqrt 2 }$$[/tex] fordi i oppgaven skal [tex]$$h > 0$$[/tex] og [tex]$$k > 0$$[/tex].
Altså jeg har x-verdien som gjør den deriverte lik null, og nå ønsker jeg å studere denne x-verdien ved bruk av fortegns-skjema (vil ikke derivere en gang til).
[tex]$${k\left[ {1 - {{3{h^2}} \over {{h^2} + 4}}} \right]{{\left( {{h^2} + 4} \right)}^{ - {3 \over 2}}}}$$[/tex]
Hver av disse faktorene må inn i utgangspunktet inn i et fortegns-skjema. Ble bare litt satt ut når jeg skulle fylle dem inn:

Legger ved oppgaven:
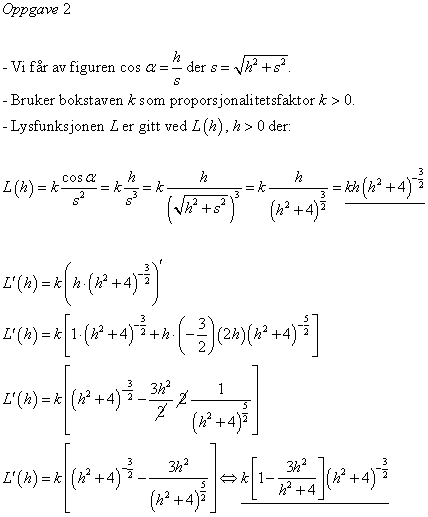


Her er min deriverte:
[tex]$${k\left[ {1 - {{3{h^2}} \over {{h^2} + 4}}} \right]{{\left( {{h^2} + 4} \right)}^{ - {3 \over 2}}}}$$[/tex]
Den har nullpunktet [tex]$${+\sqrt 2 }$$[/tex] fordi i oppgaven skal [tex]$$h > 0$$[/tex] og [tex]$$k > 0$$[/tex].
Altså jeg har x-verdien som gjør den deriverte lik null, og nå ønsker jeg å studere denne x-verdien ved bruk av fortegns-skjema (vil ikke derivere en gang til).
[tex]$${k\left[ {1 - {{3{h^2}} \over {{h^2} + 4}}} \right]{{\left( {{h^2} + 4} \right)}^{ - {3 \over 2}}}}$$[/tex]
Hver av disse faktorene må inn i utgangspunktet inn i et fortegns-skjema. Ble bare litt satt ut når jeg skulle fylle dem inn:

Legger ved oppgaven: