matematikk.net

Et ortonormert koordinatsystem betyr; aksene vinklerette på hverandre og at akse-enehetene er like.



Løsningsforslag:

Vi starter med å tegne en figur utifra opplysningene i oppgaveteksten:




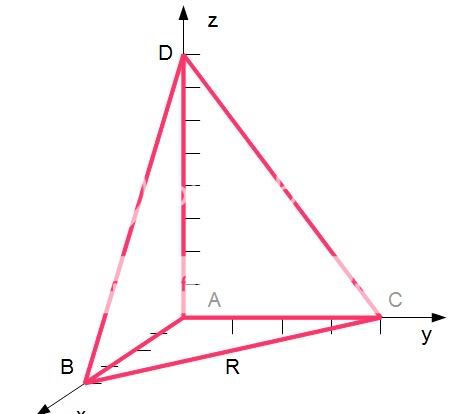
a)

[tex]$$A\left( {0,0,0} \right)$$[/tex]

[tex]$$B\left( {4,0,0} \right)$$[/tex]

[tex]$$C\left( {0,4,0} \right)$$[/tex]

[tex]$$D\left( {0,0,8} \right)$$[/tex]

[tex]$$R\left( {2,2,0} \right)$$[/tex] (sammensmelting av B og C)


[tex]$$\vec {BC} = \left[ {0 - 4,4 - 0,0 - 0} \right]$$[/tex]

[tex]$$\underline {\vec{BC} = \left[ { - 4,4,0} \right]} $$[/tex]

[tex]$$\vec{BD} = \left[ {0 - 4,0 - 0,8 - 0} \right]$$[/tex]

[tex]$$\underline {\vec{BD} = \left[ { - 4,0,8} \right]} $$[/tex]

b)

Tankegang: Jeg bruker vektorene [tex]\vec{BC}[/tex] og [tex]\vec{BD}[/tex] som jeg definerte i deloppgave A.

Ut ifra disse kan jeg bruke x-produktet og lage meg en normalvektor [tex]$$\vec N $$[/tex] som står vinkelrett på planet [tex]$$\alpha $$[/tex].

Når jeg har denne normalvektoren, bruker jeg den generelle ligningen for plan:

[tex]$$\alpha = a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) + c\left( {z - {z_0}} \right)$$[/tex]



Spørsmål: Grunnen til at jeg ikke har regnet ut B enda, er at jeg er i tvil om jeg har gjort alt riktig til nå?

Ser riktig ut det i mine øyne, hvorfor ikke?

EDIT: (Eneste jeg har å påpeke er at du skrev ortnonormert istedenfor ortonormert)

mstud wrote:Ser riktig ut det i mine øyne, hvorfor ikke?

EDIT: (Eneste jeg har å påpeke er at du skrev ortnonormert istedenfor ortonormert)

Hei mstud!

Rettet opp! Følte jeg tok en spansk en ang koordinatene. (Liker å ha alt servert, men da tar man jo også litt av morroa av det...)

Da gir jeg på med oppgave B.

b)


[tex]\vec{BD}X\vec{BC} = \left[ {0,0,16} \right][/tex] og [tex]$$B\left( {4,0,0} \right)$$[/tex]

[tex]$$\alpha:\;a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) + c\left( {z - {z_0}} \right)=0$$[/tex]

[tex]$$\alpha:\;0\left( {x - {4}} \right) + 0\left( {y - {0}} \right) + 16\left( {z - {0}} \right)=0$$[/tex]

[tex]\underline{\underline{\alpha:\;16z=0}}[/tex]

Spørsmål: Var dette en litt stusselig ligning for et plan?

Du har funnet en normalvektor som peker rett opp fra xy-planet. Da kan du se rett i fra figuren din at det må være feil! Hvordan regnet du ut kryssproduktet?

Vektormannen wrote:Du har funnet en normalvektor som peker rett opp fra xy-planet. Da kan du se rett i fra figuren din at det må være feil! Hvordan regnet du ut kryssproduktet?

Det blir slik bildet ovenfor viser. Jeg har brukt BC og BD for å lage meg en ny vektor som står vinkelrett på planet alfa.

Vektorproduktet er regnet ut ved bruk av matrisemetoden:


(bildet er kun et eksempel)

Du er ikke enig i dette?

Jada, er enig i metoden, men det ser ut som du har gjort en eller annen regnefeil. Ingen av komponentene i normalvektoren skal bli 0! (Det ser vi fra figuren også.)

Vektormannen wrote:Jada, er enig i metoden, men det ser ut som du har gjort en eller annen regnefeil. Ingen av komponentene i normalvektoren skal bli 0! (Det ser vi fra figuren også.)

Rettelse - b)

Fant feilen: Normalvektoren skal være: [tex]$$\vec {BC}X\vec{BD} = 16\left[ {2,2,1} \right]$$[/tex]

[tex]$$B\left( {4,0,0} \right)$$[/tex]

[tex]$$\alpha:\;a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) + c\left( {z - {z_0}} \right)=0$$[/tex]

[tex]\alpha:\;32\left( {x - {4}} \right) + 32\left( {y - {0}} \right) + 16\left( {z - {0}} \right)=0[/tex]

[tex]$$\alpha:\;32x - 128 + 32y + 16z = 0$$[/tex]

[tex]\underline{\underline{\alpha:\;16\left[ {2x + 2y + z - 8} \right] = 0}}[/tex]

Kommentar: Dette så litt bedre ut; hvordan visse du at jeg hadde regnet feil? Hvordan visste du at den andre normalvektoren jeg fant ikke var riktig? ("jeg bare regner jeg" )

Anta atdet første planet ditt var rett.

Da betyr dette at

\beta: 8z + 8y + 0z + 0d = 0

Dette betyr at dette planet står normalt på både x og y aksen. Altså at planet ditt er paralellt med xy planet. Altså grunnflaten i tegningen din.

Dette stemmer bra for B og C

men A faller jo helt utenfor

Forslag - c)

Normalvektoren jeg fant tidligere [tex]$$\vec {BC}X\vec{BD} = 16\left[ {2,2,1} \right]$$[/tex] er parallell med retningsvektoren til linja. Linja går igjennom origo [tex]$$A\left( {0,0,0} \right)$$[/tex]

Vi benytter oss av den generelle parameterframstilling for en rett linje:

[tex]$$x = {x_0} + at$$[/tex]
[tex]$$y = {y_0} + bt$$[/tex]
[tex]$$z = {z_0} + ct$$[/tex]

[tex]$$x = 0 + 32t \Rightarrow x = 32t$$[/tex]
[tex]$$y = 0 + 32t \Rightarrow y = 32t$$[/tex]
[tex]$$z = 0 + 16t \Rightarrow z = 16t$$[/tex]


Vi skal bestemme eventuelle skjæringspunkter mellom planet [tex]$$\alpha:\;32x + 32y + 16z-128 = 0$$[/tex] og linja l [tex]$$x = 32t \;\wedge\; y = 32t \;\wedge\; z = 16t$$[/tex]

For alle verdier av t ligger punktet [tex]\left( {32t,32t,16t} \right)[/tex] på linja. Hvis dette punktet også skal ligge i planet, må koordinatene [tex]$${32t,\;}$$[/tex] [tex]$${32t,}$$[/tex] og [tex]$${16t}$$[/tex] passe i likningen for planet:

[tex]$$32x + 32y + 16z-128 = 0$$[/tex]

[tex]$$32 \cdot \left( {32t} \right) + 32 \cdot \left( {32t} \right) + 16 \cdot \left( {16t} \right) - 128 = 0$$[/tex]

[tex]$$1024t + 1024t + 256t - 128 = 0$$[/tex]

[tex]$$2304t = 128$$[/tex]

[tex]$$t = {{128} \over {2304}} = \underline {{1 \over {18}}} $$[/tex]


Dette viser at punktet [tex]\left( {32t,32t,16t} \right)[/tex] ligger i planet når [tex]$$t = {1 \over {18}}$$[/tex].

Så setter vi parameterverdien inn i parameterframstillingen:

[tex]$$x = 32 \cdot \left( {{1 \over {18}}} \right) = {{16} \over 9}\; \wedge \;y = 32 \cdot \left( {{1 \over {18}}} \right) = {{16} \over 9}\; \wedge \;z = 16 \cdot \left( {{1 \over {18}}} \right) = {8 \over 9}$$[/tex]

Skjæringspunktet har altså koordinatene [tex]$$\left( {{{16} \over 9},{{16} \over 9},{8 \over 9}} \right)$$[/tex]

Kommentar: Fant en fremgangsmåte på nettet, men føler kanskje svarene mine burde vært heltall? Ergo føler jeg har gjort en feil et sted. Men men, lærer mye av dette hvertfall!

Regningen din ser riktig ut den!

Men jeg har en liten kommentar. Du har valgt 16[2,2,1] som normalvektoren, men du kunne like godt valgt [2,2,1]. Det som er viktig med normalvektoren er hvilken retning den har. Hvor lang den er har ingenting å si. Tallet 16 vil bare gjøre vektoren 16 ganger lengre. Det er ingenting galt i det, men det gjør regningen unødvendig tung, siden tallene blir større. Hadde du valgt [2,2,1] som normalvektor ville du fått at planet er gitt ved [tex]2x + 2y + 16z - 8 = 0[/tex] og linja ville blitt [tex](x,y,z) = (2t, 2t, t)[/tex]. Regningen ville videre blitt helt lik, men du ville fått mye mindre tall å håndtere. (Du ville fått en litt annen t-verdi, men til slutt ville du endt opp med samme punkt.)

En annen kommentar er at når du har en slik planligning som du har fått her, så er det alltid lurt å forkorte den mest mulig. Hvis du deler på 16 på hver side så får du [tex]2x + 2y + z - 8 = 0[/tex]. Denne beskriver nøyaktig samme plan (som du ser ovenfor ville du fått denne om du valgte [2,2,1] som normalvektor.)

Vektormannen wrote:Regningen din ser riktig ut den!

Men jeg har en liten kommentar. Du har valgt 16[2,2,1] som normalvektoren, men du kunne like godt valgt [2,2,1]. Det som er viktig med normalvektoren er hvilken retning den har. Hvor lang den er har ingenting å si. Tallet 16 vil bare gjøre vektoren 16 ganger lengre. Det er ingenting galt i det, men det gjør regningen unødvendig tung, siden tallene blir større. Hadde du valgt [2,2,1] som normalvektor ville du fått at planet er gitt ved [tex]2x + 2y + 16z - 8 = 0[/tex] og linja ville blitt [tex](x,y,z) = (2t, 2t, t)[/tex]. Regningen ville videre blitt helt lik, men du ville fått mye mindre tall å håndtere. (Du ville fått en litt annen t-verdi, men til slutt ville du endt opp med samme punkt.)

En annen kommentar er at når du har en slik planligning som du har fått her, så er det alltid lurt å forkorte den mest mulig. Hvis du deler på 16 på hver side så får du [tex]2x + 2y + z - 8 = 0[/tex]. Denne beskriver nøyaktig samme plan (som du ser ovenfor ville du fått denne om du valgte [2,2,1] som normalvektor.)

En kjempeflott tilbakemelding Vektormannen!

Skal fikse opp i deloppgave C og legge ut et løsningsforslag til deloppgave D. Dette blir saker! (tenkte hvis jeg lager komplette løsningsforslag til alle tidligere eksamensett jeg finner - bør jeg ha stålkontroll når eksamen kommer)

Forslag - d)

For å bestemme avstanden fra punktet [tex]$$A\left( {0,0,0} \right)$$[/tex] (origo) til planet [tex]$$\alpha:\;2x + 2y + 16z-8 = 0$$[/tex] med normalvekter [tex]$$\vec {n} = \left[ {2,2,1} \right]$$[/tex].


Bruker vi formelen; Avstand fra punkt til plan: [tex]$$q = {{\left| {a{x_1} + b{y_1} + c{z_1} + d} \right|} \over {\sqrt {{a^2} + {b^2} + {c^2}} }}$$[/tex]

[tex]$$q = {{\left| {2 \cdot 0 + 2 \cdot 0 + 16 \cdot 0 - 8} \right|} \over {\sqrt {{2^2} + {2^2} + {{16}^2}} }}$$[/tex]

[tex]$$q = {8 \over {2\sqrt {66} }} \approx \underline{\underline {0.5}} $$[/tex]

Kommentar: Siste del av deloppgave C får jeg kose meg med i morgen. Takk alle for hjelpen så lenge.

Det ser nesten riktig ut det. Du slurver litt med z-koordinaten. Den skal være 1, ikke 16?

Et annet forslag er å benytte det du fant i c). Slik du gjør det nå (ikke misforstå, det er helt riktig å gjøre det slik også) så kommer denne avstandsformelen ut av det blå. De tidligere deloppgavene bygger på en måte opp til at du kan finne denne avstanden uten å benytte formelen. Det du har gjort i forrige deloppgave er å finne det punktet i planet hvor linja som går gjennom origo og som står normalt på planet treffer planet. Korteste avstand fra et punkt til et plan er jo nettopp lengden av linjestykket fra punktet som treffer normalt på planet, ikke sant? Hvis jeg skal gå fra et punkt til et plan så treffer jeg jo planet først dersom jeg går i en rett linje rett mot planet, og ikke på skrå mot planet.

Avstanden fra A til planet er altså avstanden fra A til skjærinspunktet som du fant i forrige deloppgave!

Vektormannen wrote:Avstanden fra A til planet er altså avstanden fra A til skjærinspunktet som du fant i forrige deloppgave!

Dette forstår jeg og det er jo en typisk "algoritme"/"oppskrift" for hvordan læreren bygger opp oppgavene - at man bruker informasjonen man finner videre.

finner skjæringspunket fra c:

[tex]$$2x + 2y + z - 8 = 0$$[/tex]

[tex]$$2 \cdot \left( {2t} \right) + 2 \cdot \left( {2t} \right) + 1 \cdot \left( t \right) - 8 = 0$$[/tex]

[tex]$$4t + 4t + t = 8$$[/tex]

[tex]$$\underline {t = {8 \over 9}} $$[/tex]

[tex]$$x = 2 \cdot \left( {{8 \over 9}} \right)\; \wedge \;y = 2 \cdot \left( {{8 \over 9}} \right)\; \wedge \;z = 1 \cdot \left( {{8 \over 9}} \right)$$[/tex]

[tex]$$S = \left( {{{16} \over 9},{{16} \over 9},{8 \over 9}} \right) \Leftrightarrow \underline {\left( {{2 \over 9},{2 \over 9},{1 \over 9}} \right)} $$[/tex]


Nå bruker vi skjæringspunktet [tex]\left( {{2 \over 9},{2 \over 9},{1 \over 9}} \right)[/tex] og [tex]A\left( {0,0,0} \right)[/tex].

Litt skeptisk til dette skjæringspunktet.


forslag 2 - d:

Vi benytter oss av; avstandsformelen:

[tex]$$AS = \sqrt {{{\left( {{2 \over 9} - 0} \right)}^2} + {{\left( {{2 \over 9} - 0} \right)}^2} + {{\left( {{1 \over 9} - 0} \right)}^2}} $$[/tex]

[tex]$$\underline {AS = {1 \over 3}} $$[/tex]

Her kunne jeg (og burde kanskje på eksamen) regnet ut [tex]$$\vec{AS} $$[/tex] og deretter lengden av denne vektoren; [tex]$$\left| {x,y} \right| = \sqrt {{x^2} + {y^2}} $$[/tex]. Avstandsformelen er vel bare en sammensmeltning av disse to grunnformlene.

[tex]$$\vec{AS} = \left[ {{2 \over 9} - 0,{2 \over 9} - 0,{1 \over 9} - 0} \right]$$[/tex]

[tex]$$\left| {\vec{AS} } \right| = \sqrt {{{\left( {{2 \over 9}} \right)}^2} + {{\left( {{2 \over 9}} \right)}^2} + {{\left( {{1 \over 9}} \right)}^2}} = \underline {{1 \over 3}} $$[/tex]

Kommentar: Er ikke helt fortrolig med punktene til skjæringspunktet, føler på meg at disse burde vært mer heltall? Kan jeg gange ut 9? Det går vel ikke... - men det nærmer seg!