matematikk.net

Løsningsforslag:
a)

Vi starter med å tegne en figur av opplysningene ovenfor


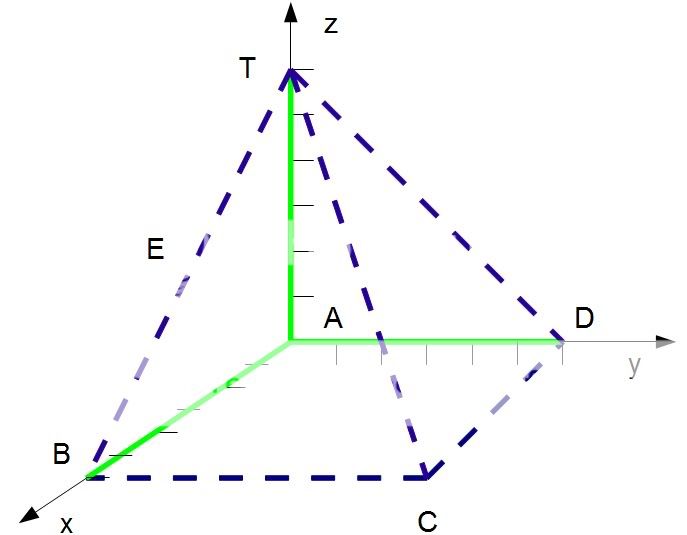
[tex]$$A\left( {0,0,0} \right)$$[/tex]

[tex]$$B\left( {6,0,0} \right)$$[/tex]

[tex]$$\underline{\underline {C\left( {6,6,0} \right)}} $$[/tex]

[tex]$$\underline{\underline {D\left( {0,6,0} \right)}} $$[/tex]

[tex]$$\underline{\underline {T\left( {0,0,6} \right)}} $$$[/tex]

[tex]$$\vec{AC} = \left[ {6 - 0,6 - 0,0 - 0} \right] = \underline{\underline {\left[ {6,6,0} \right]}} $$[/tex]

[tex]$$\vec{CT} = \left[ {0 - 6,0 - 6,6 - 0} \right] = \left[ { - 6, - 6,6} \right] \Leftrightarrow \underline{\underline {\left[ { - 1, - 1,1} \right]}} $$[/tex]

[tex]$$\vec{BT} = \left[ {0 - 6,0 - 0,0 - 0} \right] = \underline{\underline {\left[ { - 6,0,0} \right]}} $$[/tex]

[tex]$$\vec{AE} = \vec{AB} + BE$$[/tex]

[tex]$$\vec{AE} = \vec{AB} + {1 \over 2} \cdot \vec{BT} $$[/tex]

[tex]$$\vec{AE} = \left[ {6 - 0,0 - 0,0 - 0} \right] + {1 \over 2} \cdot \left[ { - 6,0,0} \right]$$[/tex]

[tex]$$\vec{AE} = \left[ {6,0,0} \right] + \left[ { - 3,0,0} \right]$$[/tex]

[tex]$$\vec{AE} = \left[ {6 + \left( { - 3} \right),0 + 0,0 + 0} \right] = \underline{\underline {\left[ {3,0,0} \right]}} $$[/tex]


Kommentar: Har jeg tegnet figuren riktig? Føler grunnflaten min ligner mer på en rombe: http://no.wikipedia.org/wiki/Rombe enn et kvadrat: http://no.wikipedia.org/wiki/Kvadrat. Jeg føler uansett at figuren må se slik ut!

Jada, det ser nesten helt riktig ut dette.

For min del ser nå grunnflaten helt kvadratisk ut? (Hvis man ikke ser tegningen i riktig perspektiv så ser det jo såklart ut som en rombe :p)

Det eneste jeg har å pirke på er denne ekvivalenspilen du kommer med. For det første så gir det ingen mening å sette en ekvivalenspil mellom to vektorer. Ekvivalenspilen setter man mellom to logiske uttrykk, f.eks. to ligninger eller andre logiske utsagn. Å sette det mellom to vektorer gir ingen mening! Men det er heller ikke riktig å si at [tex]\vec{CT} = [-1,-1,1][/tex] hvis det er noe sånt du mener. Hva mener du egentlig?

Vektormannen wrote:Jada, det ser nesten helt riktig ut dette.

For min del ser nå grunnflaten helt kvadratisk ut? (Hvis man ikke ser tegningen i riktig perspektiv så ser det jo såklart ut som en rombe :p)

Det eneste jeg har å pirke på er denne ekvivalenspilen du kommer med. For det første så gir det ingen mening å sette en ekvivalenspil mellom to vektorer. Ekvivalenspilen setter man mellom to logiske uttrykk, f.eks. to ligninger eller andre logiske utsagn. Å sette det mellom to vektorer gir ingen mening! Men det er heller ikke riktig å si at [tex]\vec{CT} = [-1,-1,1][/tex] hvis det er noe sånt du mener. Hva mener du egentlig?

[tex]$$\vec{CT} = \left[ {0 - 6,0 - 6,6 - 0} \right] = \left[ { - 6, - 6,6} \right] \Leftrightarrow \underline{6\underline {\left[ { - 1, - 1,1} \right]}} $$[/tex]

Det var meningen å se litt proff ut her... Dropper ekvivalenstegnet her...

Trodde jeg kunne skrive den som: [tex]\vec{CT} = [-1,-1,1][/tex]
Det er jo dette med at det ikke er vits å oppgi en vektor 6 ganger så lang?? Du har jo akkurat lært meg det

[tex]\vec{CT}[/tex] betyr vektoren som peker fra punktet C til punktet T. En vektor har en lengde og en retning. Det er ikke lenger samme vektor om den ikke har korrekt lengde. Vektoren [-1, -1, 1] peker i samme retning, men den er altså ikke lang nok. Da kan du ikke si at det er [tex]\vec{CT}[/tex]. (Om du vil kan du som du gjorde ovenfor skrive den som [tex]\vec{CT} = 6[-1,-1,1][/tex].)

Vektormannen wrote:[tex]\vec{CT}[/tex] betyr vektoren som peker fra punktet C til punktet T. En vektor har en lengde og en retning. Det er ikke lenger samme vektor om den ikke har korrekt lengde. Vektoren [-1, -1, 1] peker i samme retning, men den er altså ikke lang nok. Da kan du ikke si at det er [tex]\vec{CT}[/tex]. (Om du vil kan du som du gjorde ovenfor skrive den som [tex]\vec{CT} = 6[-1,-1,1][/tex].)

I rest my case Men jeg kunne gjort det feks med en normalvektor (den trenger jo ingen spesiel lengde) sant?

Kjempeflott at du tar deg tid til dette Vektormannen, du gjør deg verdig ditt nickname

Akkurat. Når du skal finne en vektor mellom to punkt så må denne ha korrekt retning og korrekt lengde. Det skal jo være en vektor som du skal kunne plassere i startpunktet, og da skal den peke helt til det andre punktet.

Når du f.eks. skal finne en normalvektor til et plan så er det ingen andre krav til vektoren enn at den skal ha en retning som er normal på planet. Hvor lang den er spiller ingen rolle. Derfor kan man da velge seg en vektor med ønsket lengde som normalvektoren, f.eks. en vektor som gir små tall som koordinater.

b)

[tex]$$\vec{AF} = \vec{AC} + {2 \over 3}\vec{CT} $$[/tex]

[tex]$$\vec{AF} = \left[ {6,6,0} \right] + {2 \over 3}\left[ { - 6, - 6,6} \right]$$[/tex]

[tex]$$\vec{AF} = \left[ {6,6,0} \right] + \left[ { - 4, - 4,4} \right]$$[/tex]

[tex]$$\vec{AF} = \left[ {6 + \left( { - 4} \right),6 + \left( { - 4} \right),0 + 4} \right]$$[/tex]

[tex]$$\underline {\vec{AF} = \left[ {2,2,4} \right]} $$[/tex]


[tex]$$\vec{AF} \bot \vec{CT} \Leftrightarrow \vec{AF} \cdot \vec{CT} = 0$$[/tex]

[tex]$$\vec{AF} \cdot \vec{CT} = \left[ {2,2,4} \right] \cdot \left[ { - 6, - 6,6} \right]$$[/tex]

[tex]$$\vec{AF} \cdot \vec{CT} = \left( {2 \cdot \left( { - 6} \right) + 2 \cdot \left( { - 6} \right) + 4 \cdot 6} \right)$$[/tex]

[tex]$$\underline{\underline {\vec{AF} \cdot \vec{CT} = 0}} $$[/tex]


c)

[tex]$${V_{parallellepiped}} = \left| {\left( {\vec{a} \times \vec{b} \right) \cdot \vec{c } \right|$$[/tex]

[tex]$${V_{pyramide\;kvadratisk\;grunnflate}} = {1 \over 3}\left| {\left( {\vec{a} \times \vec{b } \right) \cdot \vec{c } \right|$$[/tex]

Kommentar: Er dere enige i formlene mine? Jeg gjettet meg litt til den andre, mener på at den skal være riktig. Gjelder det her å huske den første og deretter kunne utlede hva man trenger fra den?

c)

[tex]$${V_{pyramide}} = {1 \over 3}\left| {\left( {\vec{AF} \times \vec{CT} } \right) \cdot \vec{BT} } \right|$$[/tex]

[tex]$$\vec{AF} \times \vec{CT} \Rightarrow \left[ {36, - 36,0} \right] = 18\left[ {2, - 2,0} \right]$$[/tex]

Hadde jeg her kun brukt [tex]$$\left[ {2, - 2,0} \right]$$[/tex] som kryss-produkt og regnet videre, hadde jeg ikke fått samme volum. Det vil altså si at jeg er nødt til å bruke hele vektoren (lengde og retning!)

Enig Vektormannen?

[tex]$${V_{pyramide}} = {1 \over 3}\left| {\left[ {36, - 36,0} \right] \cdot \left[ { - 6,0,0} \right]} \right|$$[/tex]

[tex]$${V_{pyramide}} = {1 \over 3}\left| { - 216} \right| = {{216} \over 3} = \underline{\underline {72}} $$[/tex]

Svaret ditt er riktig, men jeg ser ikke helt hvorfor du krysser [tex]\vec{AF}[/tex] med [tex]\vec{CT}[/tex]? Det gir riktig svar, men såvidt jeg kan se er det egentlig tilfeldigvis rett. I uttrykket [tex]V = |(\vec{a} \times \vec{b}) \cdot \vec{c}|[/tex] så skal vektorene [tex]\vec{a}[/tex], [tex]\vec{b}[/tex] og [tex]\vec{c}[/tex] peke fra samme punkt og langs tre av sidene i pyramiden. F.eks. i dette tilfellet: [tex]V = \frac{1}{3}|(\vec{AB} \times \vec{AC}) \cdot \vec{AT}|[/tex]. (Det er heller ingenting i veien for at du kan regne volumet uten å bruke vektorer i det hele tatt. Volumet av en pyramide er 1/3 av arealet av grunnflaten ganger høyden. Her er det lett å finne både grunnflateareal og høyde!)

Når det gjelder kommentarene dine så er det siste du sier der riktig. Du kunne ikke tatt vektoren [2,-2,0] i stedet for 18[2,-2,0]. Volumformelen sier nøyaktig hvilket kryssprodukt du skal bruke for å regne ut volumet. Hvis du tar en vektor i samme retning men med annen lengde så bruker du jo ikke den samme vektoren lenger.

Jeg er enig i formlene dine. Som du sier er det bare å huske på parallellepipedformelen, og så vil andre formler følge rett fra den. Det kan være lurt å sette seg litt inn i hvorfor formelen er som den er, altså hva den egentlig betyr. Da kan det være lettere å finne formelen til volumet av andre figurer.

Vektormannen wrote:Svaret ditt er riktig, men jeg ser ikke helt hvorfor du krysser [tex]\vec{AF}[/tex] med [tex]\vec{CT}[/tex]? Det gir riktig svar, men såvidt jeg kan se er det egentlig tilfeldigvis rett. I uttrykket [tex]V = |(\vec{a} \times \vec{b}) \cdot \vec{c}|[/tex] så skal vektorene [tex]\vec{a}[/tex], [tex]\vec{b}[/tex] og [tex]\vec{c}[/tex] peke fra samme punkt og langs tre av sidene i pyramiden. F.eks. i dette tilfellet: [tex]V = \frac{1}{3}|(\vec{AB} \times \vec{AC}) \cdot \vec{AT}|[/tex]. (Det er heller ingenting i veien for at du kan regne volumet uten å bruke vektorer i det hele tatt. Volumet av en pyramide er 1/3 av arealet av grunnflaten ganger høyden. Her er det lett å finne både grunnflateareal og høyde!)

Når det gjelder kommentarene dine så er det siste du sier der riktig. Du kunne ikke tatt vektoren [2,-2,0] i stedet for 18[2,-2,0]. Volumformelen sier nøyaktig hvilket kryssprodukt du skal bruke for å regne ut volumet. Hvis du tar en vektor i samme retning men med annen lengde så bruker du jo ikke den samme vektoren lenger.

Jeg er enig i formlene dine. Som du sier er det bare å huske på parallellepipedformelen, og så vil andre formler følge rett fra den. Det kan være lurt å sette seg litt inn i hvorfor formelen er som den er, altså hva den egentlig betyr. Da kan det være lettere å finne formelen til volumet av andre figurer.

Et kjempe tilbakemelding, tusen takk Vektormannen.

Hvorfor jeg har valgt AF X CT vet ikke jeg heller (det gikk tydeligvis litt for eller litt for seint, et eller annet, for dette kan jeg!)

En liten siste kommentar (siden du er hva du heter: Vektormannen); vi har akkurat begynt på matriser i matematikken, skommet litt i boken og aner at de matrisene vi regner ut nå, kan brukes til å bestemme volumet de også?

Fortsatt god kveld!

Ja, matriser kan brukes for å beregne volumet også. Eller rettere sagt, determinantene av matrisene. Vi har nemlig at [tex](\vec{a} \times \vec{b}) \cdot \vec{c} = \left|\begin{array}{ccc} a_x & a_y & a_z\\ b_x & b_y & b_z\\ c_x & c_y & c_z\end{array}\right|[/tex]. (Her er [tex]a_x[/tex] x-komponenten til [tex]\vec{a}[/tex] og så videre. Rette streker betyr determinant.) Hvis det var noe sånt du tenkte på?

Vektormannen wrote:Ja, matriser kan brukes for å beregne volumet også. Eller rettere sagt, determinantene av matrisene. Vi har nemlig at [tex](\vec{a} \times \vec{b}) \cdot \vec{c} = \left|\begin{array}{ccc} a_x & a_y & a_z\\ b_x & b_y & b_z\\ c_x & c_y & c_z\end{array}\right|[/tex]. (Her er [tex]a_x[/tex] x-komponenten til [tex]\vec{a}[/tex] og så videre. Rette streker betyr determinant.) Hvis det var noe sånt du tenkte på?

Det var akkurat noe slikt jeg tenkte på Vi har det i pensum (matriser), foreløbig virker det som litt som å løse soduko?

Virkeligheten slår meg vel snart hardt i fjeset - matriser er ikke soduko

Hehe, blir ikke fullt så vanskelig som sudoku etter hvert :p

Razzy wrote: Det var akkurat noe slikt jeg tenkte på Vi har det i pensum (matriser), foreløbig virker det som litt som å løse soduko?

Virkeligheten slår meg vel snart hardt i fjeset - matriser er ikke soduko

Vektormannen wrote: Hehe, blir ikke fullt så vanskelig som sudoku etter hvert :p

@Razzy: Matriser og sudoku... Du skulle hatt sudoku også i pensum Men tror ikke det virker i lengden å regne ut en matrise som å fylle ut en sudoku oppgave ...



@Vektormannen: Sudoku blir heller ikke fullt så vanskelig som matriser etter hvert
Det kommer gjerne an på hva man øver mest på, hehe




Jeg har gjort litt over 350 sudoku i løpet av de (fem?) siste årene, så jeg vet hva jeg snakker om der... Kjøpte meg "Den store sudokuboken" med over 600 oppgaver for en delår siden, og så langt er jeg kommet nå (Og har selvfølgelig ikke gjort sudoku hele tiden siden, da hadde jeg vært ferdig med boka for lenge siden).

Har imidlertid ikke regnet ut så mange som 350 matriser enda... (Sikkert færre enn 100 foreløpig)