Page 1 of 1
Vektorprodukt
Posted: 28/10-2012 13:37
by HåpløsSOS
Jeg skal vise at
Ivektor u x vektor vI^2 = Ivektor uI^2 Ivektor vI^2 - (vektor u * vektor v)^2.
Hvordan skal jeg gripe dette an? Får jeg bruk for definisjonen
Ivektor u x vektor vI = Ivektor uI * Ivektor vI * sin a ?
Posted: 28/10-2012 13:45
by Vektormannen
Ja, når du skal vise noe slikt må du alltid gå til definisjonene. Det er jo disse som sier hva [tex]\vec{u} \times \vec{v}[/tex] og [tex]\vec{u} \cdot \vec{v}[/tex] er.
Hvis du begynner med å skrive opp dem, ser du da en sammenheng her?
Posted: 28/10-2012 13:51
by HåpløsSOS
Hadde satt pris på et hint til.
Posted: 28/10-2012 13:53
by Vektormannen
Et hint til er den velkjente sammenhengen at [tex]\sin^2 v + \cos^2 v = 1[/tex]. Tar du det nå?

Posted: 28/10-2012 16:26
by HåpløsSOS
Nei, jeg ser fortsatt ikke sammenhengen.
Posted: 28/10-2012 16:46
by Vektormannen
Ok, hvis vi tar tak i venstresiden da: Der har vi [tex]|\vec{u} \times \vec{v}|^2 = (|\vec{u}| \cdot |\vec{v}| \cdot \sin \alpha)^2 = |\vec{u}|^2 |\vec{v}|^2 \sin^2 \alpha[/tex]. Så bruker vi sammenhengen jeg nevnte, og vi får at dette er lik [tex]|\vec{u}|^2 |\vec{v}|^2 (1 - \cos^2 \alpha)[/tex]. Men hvis du ganger inn i parentesen, hva står det der da?
Posted: 28/10-2012 17:01
by HåpløsSOS
Og der ble lyset endelig tent! Tusen takk

Posted: 28/10-2012 17:03
by HåpløsSOS
Enda et spørsmål: Romben er vel den eneste firkanten der diagonalene står vinkelrett på hverandre?
Posted: 28/10-2012 17:19
by Vektormannen
Jeg sa ja i sted, men svaret er selsvagt nei

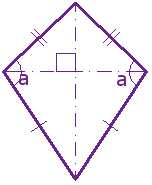
En slik "drage" er ikke en rombe, men diagonalene står vinkelrett på hverandre.
(Du kan jo starte med å tegne to linjestykker som står vinkelrett på hverandre. Uansett hvordan du gjør det så vil jo resultatet når du trekker linjestykker mellom endepunktene på diagonalene, bli en slik firkant.)
Posted: 28/10-2012 19:05
by HåpløsSOS
Takk, takk.
To plan har x-aksen som skjæringslinje. P(2,-5,1) er et punkt i det ene planet, og Q(-2,1,0) er et punkt i det andre planet. Finn vinkelen mellom planet.
Jeg antar at jeg må finne normalvektorene til planene for å vinkelen mellom dem. Men hvordan gjør jeg det? Jeg kjenner jo til et punkt og en linje (x-aksen med retningsvektor I1,0,0I) i hvert plan.
Posted: 28/10-2012 20:01
by Vektormannen
Det stemmer at du må finne normalvektoren til planene. For å finne en normalvektor til et plan krysser du to ikke-parallelle vektorer som du vet ligger i planet. Kan du finne deg to slike vektorer her?
Posted: 28/10-2012 20:02
by HåpløsSOS
Kan jeg velge to vilkårlige punkter langs x-aksen?
Posted: 28/10-2012 20:08
by Vektormannen
Ja! Alle punkter på x-aksen ligger jo i planet.

