Page 1 of 1
R1 Oppgavesamling, Oppgave 453
Posted: 27/11-2013 16:52
by Zewadir
- image.jpg (45.94 KiB) Viewed 1503 times
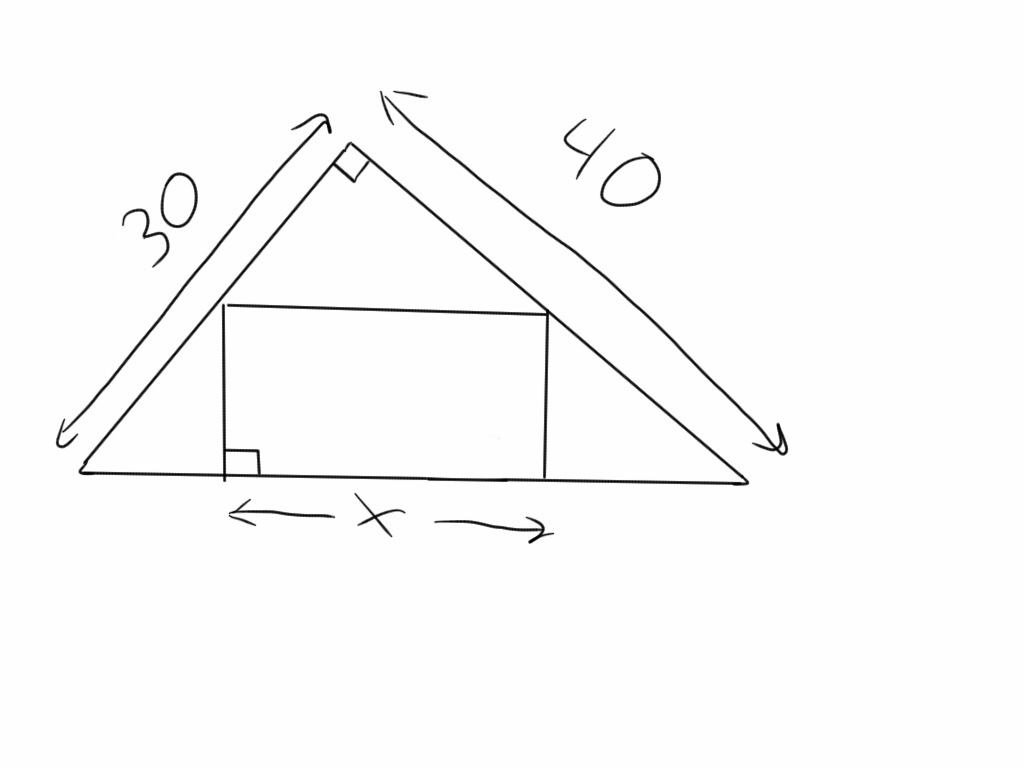
453 a) Vis at arealet av rektangelet på figuren kan skrives A(x) = 24 x - [tex]\frac{12}{25}x^{2}[/tex]
b) Finn det største arealet rektangelet kan få.
Tusen takk for all hjelp.
Re: R1 Oppgavesamling, Oppgave 453
Posted: 27/11-2013 17:02
by Nebuchadnezzar
Hva har du selv tenkt og prøvd?
Re: R1 Oppgavesamling, Oppgave 453
Posted: 27/11-2013 17:09
by Zewadir
Jeg finner at hypotenusen er 50, høyden er 24 og ser da en viss sammenheng med 24x og 12 delt på 25. Arealet av rektangelet er x multiplisert med ukjent side (f.eks. y) hvor de lengdene utenfor rektangelet er 50 - x og 24 - y. Men etter dette vet jeg ikke hvordan jeg går videre…
Trenger litt hjelp for å komme meg videre.
Re: R1 Oppgavesamling, Oppgave 453
Posted: 12/12-2013 12:17
by Guest
Bruker formlikhet mellom den største trekanten(sider 30,40, h 24) og den øverste trekanten med grunnlinje x. forholdet mellom den øverste lille trekanten og den store blir x/50, dermed blir katetene i den lille trekanten x/50*40=4x/5 og x/50*30=3x/5. Arealet av den lille øverste trekanten blir det (3x/5*4x/5)/2=12x^2/50. dermed finner vi at høyden i den lille øverste trekanten er 24x/50=12x/25. Arealet av firkanten blir da x*y, y er 24-12x/25. A=x(24-12x/25)=24x-12x^2/25