matematikk.net

Hei,
Jeg prøver å ta R1 etter å ha vært borte fra skolebenken i 12 år.
Sliter litt med funksjonen: f(x): x^4-6x^2+5
Oppgaven a går ut på: Bestem de intervaller der f(x) vokser og der f(x) minker. Vet ikke hvordan jeg går fram?
Noen tips

Vet du hva den deriverte av en graf forteller deg?

Grafen til f’(x) viser vekstforløpet til f(x) Dersom f'(x) er positiv vokser f(x) og hvis den er negativ synker f(x) Eg mener at man kan finne bunn og topppunkter slik?

Er det ingen som kan hjelpe meg.............?? Hvis jeg deriverer uttrykket blir det: f'(x)=4x^3-12x

Helt riktig! Når du setter f'(x)=0 finner du topp og bunnpunkter. Fellesbetegnelse for topp og bunnpunkter er ekstremalpunkter. Mellom to ekstremalpunkter vokser (f'(x) positivi) eller synker (f'(x) negativ) grafen (kun en av delene). Tegn fortegnslinjen til grafen, og da vil du se i hvilke intervaller f(x) vokser og i hvilke intervaller den synker. Gir dette mening for deg?

Hmmm.....
Vel, må vel inrømme at jeg er en smule *blond* og mangel på matekunskapen min er på bånn. Har aldri hatt R1 matte så har ingen knagger å henge ting på. Hadde matte for 20 år siden på videregående men det var som den gang het Matte sammfunnsfaglig. Husker ikke noe som helst, så læringskurven min er rett opp
Må nok ha det inn med ts.....

a)
Når oppgaven går ut på å bestemme intervaller for f(x) vokser og der f(x) synker detter jeg litt ut. Hvordan kan man BESTEMME det når jeg har en gitt funksjon:
f(x)= x^4 - 6x^2 + 5.
Den deriverte av f'(x) =4x^3 - 12x har jeg funnet ut.
Den 2re deriverte f''(x) = 12x - 12.
Evnt finn bunn og toppunkter.

I fasit står det at mellom intervallet vokser (-1,73,0) og i (1,73,->) og minker i (<-,-1,73) og i (0,1,73)
Hvordan kommer jeg fram til det????

b)
Bestem de intervaller der grafen til f vender den hule siden opp eller ned. Finn eventuelle vendepunkter.

c)
Tegn grafen

d)
Finn likningen for eventuelle vendetangenter.

Hjelp plz...........har holdt på med oppgaven i en hel dag og kommer ikke noe vei.......har 19 oppgaver til og må levere leksene på mandag;((((

BEKLAGER FEIL; SKAL VÆRE RIKTIG NÅ:

Du har funnet at [tex]f'(x)=4x^3-12x[/tex]. Som du sier, kan vi nå finne topp og bunnpunkter ved sette [tex]f'(x)=0[/tex]. Vi får:

[tex]4x^3-12x=0[/tex]

[tex]4x(x^2-3)=0[/tex]

[tex]x=0[/tex] eller [tex]x^2-3=0[/tex]

[tex]x=0[/tex] eller [tex]x=\pm \sqrt{3}[/tex]

Er du enig dette (du kan kontrollere ved å erstatte x med 0 eller [tex]\pm \sqrt{3}[/tex] og se at den deriverte da blir lik null)?

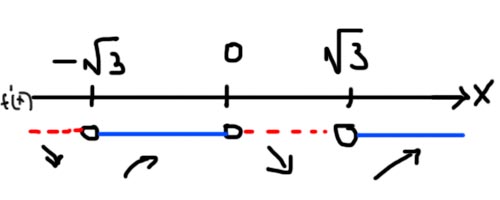
Nå har vi at [tex]f(x)[/tex] har toppukt og bunnunkt der x er 0 og [tex]\pm \sqrt{3}[/tex]. Men ligger toppunktet ved x=0 eller er det bunnpunktet som ligger ved x=0? For å finne ut dette må vi tegne en fortegnslinje (se figur under). Da prøver du en x-verdi mindre enn den minst verdien du regnet ut ([tex]- \sqrt{3}[/tex]), f.eks [tex]-3[/tex]. Så tester du en verdi mellom de verdiene du regnet ut (altså mellom [tex]- \sqrt{3}[/tex] og 0, og mellom 0 og [tex]\sqrt{3}[/tex]), f.eks. -1 og 1. Til slutt tester du en verdi større en den største du fant ([tex]\sqrt{3}[/tex]), f.eks. 5. Da får du blandt annet følgende resultater:

[tex]f'(-3)=72[/tex] (negativt)

[tex]f'(-1)=8[/tex] (positivt)

[tex]f'(1)=-8[/tex] (negativt)

[tex]f'(5)=440[/tex] (positivt)

Det viktigste er ikke hvilket tall du får, men fortegnet til tallet. Positive tall indikerer at grafen stiger, mens negative tall indikerer at den synker. Altså synker grafen før [tex]x=-\sqrt{3}[/tex], den stiger mellom [tex]x=-\sqrt{3}[/tex] og [tex]x=0[/tex], så synker den igjen mellom [tex]x=0[/tex] og [tex]x=\sqrt{3}[/tex]. Til slutt vokser den hele tiden etter [tex]x=\sqrt{3}[/tex] Dette er illustrert med fortegnslinjen under. Forstår du dette?

Når du skal finne når grafen vender sin hule side opp/ned, gjør du det samme, men dobbeltderiverer først. Altså dobbeltderiverer f(x), setter f''(x)=0, løser likningen, tester verdier under den laveste, mellom verdiene du finner, og over den største verdien, før du til slutt tegner fortegnslinjer og ser i hvilke intervaller den dobbeltderiverte er positiv/negativ (positiv - hule siden opp, negativ - hule siden ned).

PS: Mange lager R1-videoer på youtube; søk etter f.eks. "fortegnslinje R1" eller "drøfte funksjoner R"
PS: En kan ikke forvente umiddelbart svar på forumet, så etikette å ikke mase

For å illustrere at grafen synker, stipler en linjen der den er negativ:

Den deriverte av f'(x) =4x^3 - 12x har jeg funnet ut. Ikke 3x^2-12 som du har gått ut fra.....
Hovedproblemet mitt ligger akkurat der....når jeg har en tredjegradsfunksjon hva gjør jeg da?

Gitt funksjon er som jeg skrev tidligere: f(x)= x^4 - 6x^2 + 5.

Det du skrev i hvertfall var forståelig og oversiktlig.

Ikke meningen å mase, skjønner at det kan ta tid på forumet
Takk for at du tar deg tid til å skrive til meg
Ikke helt enkelt å *vekke opp* hjernecellene fra 20 års dvale.....

Så det selv - gikk litt fort i svingene . Skal være rett nå (håper jeg).

PS: Hvis du skriver tex før og tex/ etter, begge deler omsluttet av [ ], likningene og mattetegnene dine, ser det proffere ut Eks: blir [tex]4x^2[/tex]

Hei,
Hvis du har vært vekke fra matte lenge så har du sikkert ikke sett alle de utrolig bra verktøyene som finnes for å gjøre livet ditt enklere. Hadde selve vært vekke fra matte inntil barna mine begynte å spørre meg.
Her er noen, og andre kan sikkert legge til flere.

Desmos.com gjør dette tilen lek. Jeg la inn funksjonen med de deriverte: https://www.desmos.com/calculator/i2fnm4e9yv
Du kan klikke foran funksjonene for å slå de på og av.

http://www.wolframalpha.com/input/?i=+f ... 6x%5E2%2B5 er også utrolig omfattende. lim inn "f(x)=x^4-6x^2+5", og "slope of f(x)=x^4-6x^2+5" og se hva svaret blir. Det er kanskje klarere enn alle svar du fikk her på matematikk.net Det inkluderer minima, maxima, globale minima og maxima, bilder av funksjonen etc etc, og du kan klikke deg så dypt du vil.

http://www.geogebra.org/cms/nb/ er også ett fint lite program til geometri

En god kalkulator med grafer er bra hvis du må ta noe med til en eksamen.

Hei,

Takk for god informasjon og gode tips.
Synes selv at det du skrev her (forklaringen) var veldig fin. Fikk løst oppgaven. Og ikke minst forstod jeg hva jeg drev med.
Det er mange hjelpemidler man kan sette inn funksjonen i. Jeg må hele tiden prøve å forstå for å kunne løse oppgaven, og der synes jeg forum som dette kan være løsningen. Som regel er det en liten ting som gjør at en sitter fast og hvis det er noen hyggelige mennesker der ute som kan hjelpe meg sier jeg bare JA TAKK

Så tar sjansen og legger ut et nytt spørsmål:
har en brøk 2x/(x+1)^2. Dette er den første deriverte og jeg har satt den som null for å finne topp og bunnpunkt slik du lærte meg i forrige oppgave
Problemet er hvordan løser jeg denne likningen slik at jeg får x verdiene?

Lettere enn man kanskje skulle tro!

[tex]\frac{2x}{(x+1)^2}=0[/tex]

Gang med [tex](x+1)^2[/tex] på begge sider:

[tex]\frac{2x}{(x+1)^2} \cdot (x+1)^2=0 \cdot (x+1)^2[/tex]

Stryk [tex](x+1)^2[/tex] på venstresiden, og bruk at hva som helst ganget med null, fremdeles er null (på høyresiden):

[tex]2x=0[/tex]

Del begge sider på 2

[tex]x=0[/tex]

Nå bør en sjekke om nevneren (under brøkstreken) blir null når [tex]x=0[/tex]. Her gjør den ikke det, så løsningen blir [tex]x=0[/tex]. Hadde vi istedet fått [tex]x=-1[/tex], ville ikke dette vært en gyldig løsning, da nevneren ville blitt null (er jo ulovlig å dele på null!). Men igjen, her er ikke det noe problem

PS: Som Viking skrev, er Wolframalpha.com et fantastisk vektøy. Skriv f.eks. inn "solve 2x/(x+1)^2=0 for x" (kunne også bare ha skrevet likningen), og du får: http://www.wolframalpha.com/input/?i=so ... %5E2+for+x

Har du derivert, og lurer på om du deriverte riktig, kan du i Wolframalpha f.eks skrive "derivative of <utrykket ditt>".

oops!

Ser at jeg har tastet feil ..........under brøkstreken er det (x^2+1)^2-------prøvde å regne det ut og kom fram til at det er samme som : x^4+2x^2+1.
Jeg kan jo ikke derivere den for å finne x?

Ser at svaret blir uansett x=0......hehe.....
Tror det begynner å bli sent så hjernen fungerer ikke nå. Får jobbe videre i morgen og komme og *plage* dere smartinger med *glupe* spørsmål.
Tusen takk skal dere ha for å hjelpe meg