matematikk.net

Sliter virkelig med oppgaven under, og håper noen har noen tips? På forhånd takk!

En rett sirkulær sylinder skal innskrives i en rett sirkulær kjegle. Finn målene til sylinderen med maksimalt volum når kjeglen har høyde h og radius r i grunnflaten.

Om det er til noe hjelp, så skal svaret være:
Høyde: [tex]\frac{h}{3}[/tex]
Radius: [tex]\frac{2r}{3}[/tex]

Hvis du lager ei skisse av en sirkulær kjegle med en innskrevet sylinder, så kan den f eks plasseres i et koordinatsystem. Da vil sylinderen tangere sidekanten på kjegla. Så kan du prøve å finne den lineære funksjonen (y = ax + b) til kjeglas sidekant. 2 punkter trengs. Der y er sylinderens høyde og x er den radius. For y < h og x < r.

Kanskje noen kan legge inn en skisse/tegning...

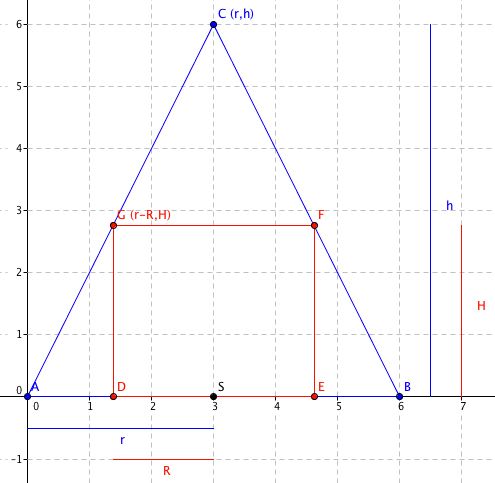
Her er hvertfall en skisse i 2D
Men når jeg skulle bruke punktene(her: G og C) til å finne den lineære funksjonen ble alt bare krøll...

Rotet mitt kom da jeg skrev: [tex]H = \frac{h-H}{R}*r[/tex]. Og om jeg hadde brukt punktet (0,0) istede for G så fikk jeg [tex]H=h[/tex] så da skjønte jeg at jeg har bommmet noe kraftig.


Har helt sikkert misforstått tipset, for føler meg veldig på bærtur

Tromla wrote:Her er hvertfall en skisse i 2D
Men når jeg skulle bruke punktene(her: G og C) til å finne den lineære funksjonen ble alt bare krøll...
Rotet mitt kom da jeg skrev: [tex]H = \frac{h-H}{R}*r[/tex]. Og om jeg hadde brukt punktet (0,0) istede for G så fikk jeg [tex]H=h[/tex] så da skjønte jeg at jeg har bommmet noe kraftig.
Har helt sikkert misforstått tipset, for føler meg veldig på bærtur

Skissa di er fin den!.
Jeg kaller S = (0, 0) og B = (r, 0) og C = (0, h). Da blir den retta linja for sidekanten på kjegla: [tex]y=(-h/r)x + h[/tex]
x: radius cyl og y: høyde cyl
slik at [tex]V(cyl) =\pi*x^2*y= \pi*x^2* \left(\frac{-h}{r}x + h\right)=-\pi(h/r)x^3 + \pi*x^2h[/tex]
så deriverer og setter lik null, for å finne max V(cyl), Dvs

[tex]V ' (cyl) =-3\pi(h/r)x^2 + 2\pi*xh=0[/tex]
så
[tex]x=\frac{2r}{3}[/tex]
og
[tex]y=\frac{h}{3}[/tex]


som ønska

Aha! Skjønte det nå! Tusen takk for hjelpen