Page 1 of 1
Beregne Lim... utgangspunkt i rekkeutviklingen for e^x
Posted: 04/05-2014 18:57
by mattefrik
Hei!
Regner på gamle eksamensoppgaver og kom over en oppgave jeg sliter med, denne ligger det ikke ut noe løsningsforslag på. Kan noen hjelpe meg?
Beregn lim (x->0) (e^x -1-x)/x^2 ved å ta utgangspunkt i rekkeutviklingen for e^x
(Oppgaven kan også løses ved l'Hospitals regel, men det vil ikke gi uttelling her.)
Kjapt svar ønskes! På forhånd tusen takk!
Re: Beregne Lim... utgangspunkt i rekkeutviklingen for e^x
Posted: 04/05-2014 19:00
by mattefrik
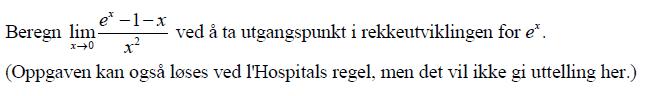
- Uten navn.jpg (12.97 KiB) Viewed 2513 times
Re: Beregne Lim... utgangspunkt i rekkeutviklingen for e^x
Posted: 04/05-2014 19:10
by Janhaa
mattefrik wrote:Uten navn.jpg
[tex]\large\lim_{x\to 0} \left(\frac{1+x-1-x+{x^2\over 2}+{x^3\over 6}+...+{x^n\over n!}}{x^2}\right)={1\over 2}[/tex]
Re: Beregne Lim... utgangspunkt i rekkeutviklingen for e^x
Posted: 04/05-2014 19:21
by mattefrik
men hvorfor blir det = 1/2 ? Med x^2 i nevneren?
Re: Beregne Lim... utgangspunkt i rekkeutviklingen for e^x
Posted: 04/05-2014 23:06
by Janhaa
mattefrik wrote:men hvorfor blir det = 1/2 ? Med x^2 i nevneren?
Taylor-rekkeutvikling av exp(x):
[tex]\lim_{x \to 0}\,\,\left((0,5x^2/x^2)\,+\,(x^3/6x^2)+... \right)[/tex]
[tex]\lim_{x \to 0}\,\,\left(0,5\,+\,(x/6)+... \right)=0,5[/tex]
Re: Beregne Lim... utgangspunkt i rekkeutviklingen for e^x
Posted: 28/10-2014 09:32
by Guest
Jeg forstår ikke dette, noen som kan forklare?
Re: Beregne Lim... utgangspunkt i rekkeutviklingen for e^x
Posted: 28/10-2014 10:25
by Nebuchadnezzar
$ \large
\begin{align*}
\lim_{x\to 0} \frac{e^x-1-x}{x^2}
& = \lim_{x\to 0}\large \left(\frac{-1-x + \bigl[x+\frac{x^2}{2}+\frac{x^3}{6}+\cdots+\frac{x^n}{n!} \bigr] }{x^2}\right) \\
& = \lim_{x\to 0} \large \left(\frac{{x^2\over 2}+{x^3\over 6}+...+{x^n\over n!}}{x^2}\right) \\
& = \lim_{x\to 0} \left( \frac{1}{2}+\frac{x}{6}+ \cdots+ \frac{x^{n-2}}{n!} \right)
\end{align*}
$