Page 1 of 1
Vinkel
Posted: 18/11-2014 12:26
by Sanding
Hei! Står litt fast på dette:
På figuren er [tex]\angle E=40^{\circ}[/tex]. Dessuten er buene AB, BC og CD like lange. Finn [tex]\angle ACD[/tex].
Jeg har funnet ut at [tex]\angle B[/tex] og [tex]\angle BCD = 70^{\circ}[/tex], men så stopper det litt opp!
Hvordan kan jeg få brukt de [tex]40^{\circ}[/tex], når det hverken er en sentral- eler periferivinkel?
Hilsen Ingrid:)
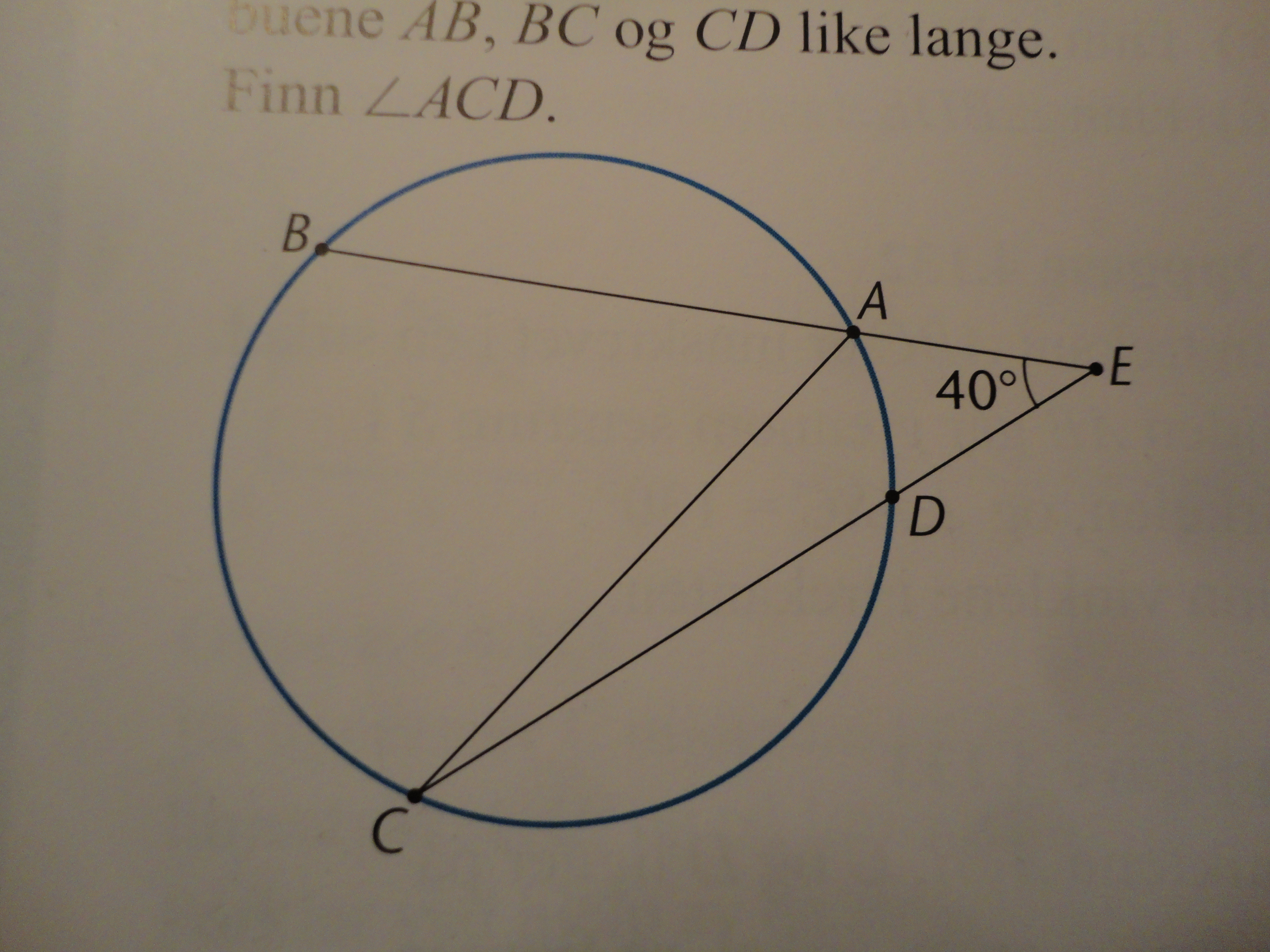
- Figur
- DSC04537.JPG (4.9 MiB) Viewed 5814 times
Re: Vinkel
Posted: 18/11-2014 14:18
by Lektorn
Du har funnet alle vinklene i trekanten BCE.
Du skal finne vinklene i trekanten CEA fordi den oppgaven spør etter ligger i denne trekanten.
Hvis du f.eks. kaller vinkel ACD=x og vinkel CAE=y, kan du finne flere uttrykk for vinkelsummer som inneholder både x og y.
I tillegg må du bruke informasjonen om sirkelbuene, som gir en del like vinkle, f.eks. BCA = CAB.
Sett sammen dette og du bør ende opp med 2 likninger med 2 ukjente som lar seg løse.
Re: Vinkel
Posted: 18/11-2014 20:37
by Sanding
Tusen takk for svar!
Høres ut som en bra løsning, men det ble litt komplisert.
Håper forstanden øker etterhvert så jeg kan forstå det!
Re: Vinkel
Posted: 18/11-2014 21:24
by Lektorn
Ja, det er komplisert så en god figur er alfa og omega for slike oppgaver.
Det er også grunnen til at det er litt vanskelig å forklare med bare tekst..
Re: Vinkel
Posted: 18/11-2014 21:28
by hallapaadeg
Regner med det er Sinus R1 du har, isåfall kan du bla èn side tilbake og se oppgaven du gjorde før den der.
Den ber deg vise et forhold som helt sikkert er veldig nyttig å huske.
b er sirkelbuen mellom de to nærmeste punktene, tilsvarende med a.

v = [tex]\frac{b-a}{2}[/tex]
Re: Vinkel
Posted: 19/11-2014 11:11
by Sanding
Weeehooo, jeg fikk det til!

Nå skulle jeg akkurat kommentere svaret og forklare hvorfor jeg ikke fikk det til, og så spratt løsningen ut av boka!
Fikk plutselig øynene opp for at når AB og BC er like lange, så er trekant ABC likebeint, og derfor må vinkel BCA og vinkel CAB være like! Og så vet jeg at vinkel B er 70 grader, og da må [tex]\angle BCA[/tex] og [tex]\angle A[/tex] være 55 grader. [tex]\angle BCD[/tex] er [tex]70^{\circ}[/tex], og da må [tex]\angle ACD[/tex] være 70-55 grader, som blir [tex]15^{\circ}[/tex], som er rett!

Tusen takk, fantastisk godt å få det til!
Re: Vinkel
Posted: 16/05-2015 21:26
by matteglad
Sliter med samme oppgave selv nå. Skjønner logikken i det meste her, men hvorfor i alle dager er ∠B=∠BCD=70∘?
Det klarer jeg ikke å se?
Re: Vinkel
Posted: 01/12-2015 20:37
by Guest
Samme her, noen som kan forklare hvorfor vinkel B er 70 grader
Re: Vinkel
Posted: 01/12-2015 20:43
by Dolandyret
Gjest wrote:Samme her, noen som kan forklare hvorfor vinkel B er 70 grader
Fordi trekanten er likebeint. Likebeinte trekanter har to like vinkler. 180-40=140 ----- 140/2=70 vinkel(B)=vinkel(C)=70 grader
Re: Vinkel
Posted: 01/12-2015 20:48
by Guest
Fordi trekant BCE er likebeint og E er 40 grader blir vinkelen BCE (180-40)/2=70 grader.
Re: Vinkel
Posted: 01/12-2015 21:26
by Guest
hvorfor tar du utgangspunkti trekant abc når man ikke vet vinkelen A? Den er 180 -x
og vinkel B C er 2x ? det er vinkel E som er 40 grader
