Page 1 of 1
Fysikk, finne retning(vinkel)
Posted: 24/01-2015 22:17
by pi-ra

- 3.7, fysikk.PNG (24.42 KiB) Viewed 1755 times
På oppgave c), når man skal finne retningen til akselerasjonen så blir det i følge fasiten [tex]-90^{\circ}[/tex].
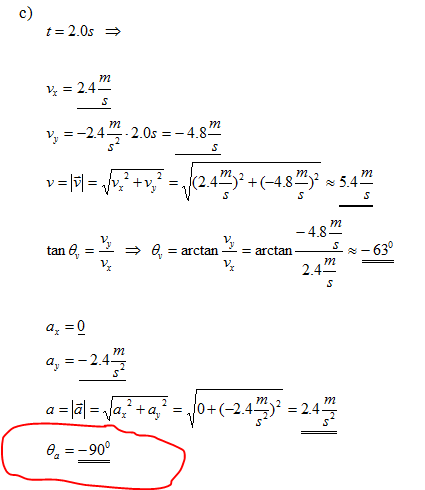
- 3.7, fysikk fasit.PNG (11.4 KiB) Viewed 1755 times
Hvorfor det? Ved utregning blir det jo [tex]\Theta = tan^{-1}(\frac{mot}{hos}) = tan^{-1}(\frac{-2.4}{0})[/tex], men det er klart at det er noe som ikke stemmer da man ikke kan ha [tex]0[/tex] i nevner.
Setter pris på alle svar.
Re: Fysikk, finne retning(vinkel)
Posted: 24/01-2015 23:43
by MatIsa
Du trenger egentlig ikke å bruke $\tan^{-1}(x)$ her, ettersom akselerasjonen i horisontal retning er 0. Da vil akselerasjonen danne en vinkel på $90^\circ$, $0^\circ$ eller $-90^\circ$ med x-aksen, avhengig av akselerasjonen i vertikal retning. Her har den vertikale akselerasjonen negativ verdi, og akselerasjonen vil derfor peke nedover og danne en vinkel på $-90^\circ$ med x-aksen.
Forresten vil $\tan^{-1}(x) \to -\frac{\pi}{2}$ når $x \to -\infty$. Så selvom du ikke kan evaluere $\tan^{-1}\left(\frac{-2.4}{0}\right)$ direkte, gir $\tan^{-1}(\frac{\text{mot}}{\text{hos}})$ mening når den hosliggende siden går nærmere og nærmere $0$
Re: Fysikk, finne retning(vinkel)
Posted: 25/01-2015 01:38
by pi-ra
MatIsa wrote:Du trenger egentlig ikke å bruke $\tan^{-1}(x)$ her, ettersom akselerasjonen i horisontal retning er 0. Da vil akselerasjonen danne en vinkel på $90^\circ$, $0^\circ$ eller $-90^\circ$ med x-aksen, avhengig av akselerasjonen i vertikal retning. Her har den vertikale akselerasjonen negativ verdi, og akselerasjonen vil derfor peke nedover og danne en vinkel på $-90^\circ$ med x-aksen.
Forresten vil $\tan^{-1}(x) \to -\frac{\pi}{2}$ når $x \to -\infty$. Så selvom du ikke kan evaluere $\tan^{-1}\left(\frac{-2.4}{0}\right)$ direkte, gir $\tan^{-1}(\frac{\text{mot}}{\text{hos}})$ mening når den hosliggende siden går nærmere og nærmere $0$
Ah, skjønner. Tusentakk!
