Page 1 of 1
Geometri-problemløsing
Posted: 29/04-2015 19:36
by stensrud
Enda en fasit som jeg synes går litt for fort frem...
I figuren nedenfor er det tegnet to sirkler med radius $8$ og $6$, der avstanden mellom sentrene deres er $12$. $P$ er midtpunktet på $QR$. Finn $QP^2$

Er det her åpenbart at den forlengede linjen mellom sentrene treffer $R$ på sirkelbuen? (Fasiten nevner ikke dette i det hele tatt, og går rett på å bruke et punkts potens for å finne svaret.)
Re: Geometri-problemløsing
Posted: 29/04-2015 19:59
by Nebuchadnezzar
Det er bare slik R er blitt definert? Altså en forlenger linjen mellom endepunktene, og kaller skjæringspunktet
med den minste sirkelen for R. Deretter trekker en linjen og avsetter Q.
Re: Geometri-problemløsing
Posted: 29/04-2015 21:55
by stensrud
Beklager, dårlig oversetting av meg... Den originale oppgaveteksten:
"In the adjoining figure, two circles with radii $6$ and $8$ are drawn with their centers $12$ units apart. At $P$, one of the points of intersection, a line is drawn in such a way that the chords $QP$ and $PR$ have equal length. ($P$ is the midpoint of $QR$) Find the area of the square with a side length of $QP$."
Det er vel egentlig bare når avstanden mellom sentrene er lik $12$ at den forlengede linjen mellom sentrene treffer $R$? F. eks når avstanden mellom sentrene er lik $10$, vil det ikke være sånn ($P$ blir ikke midtpunkt på $QR$):
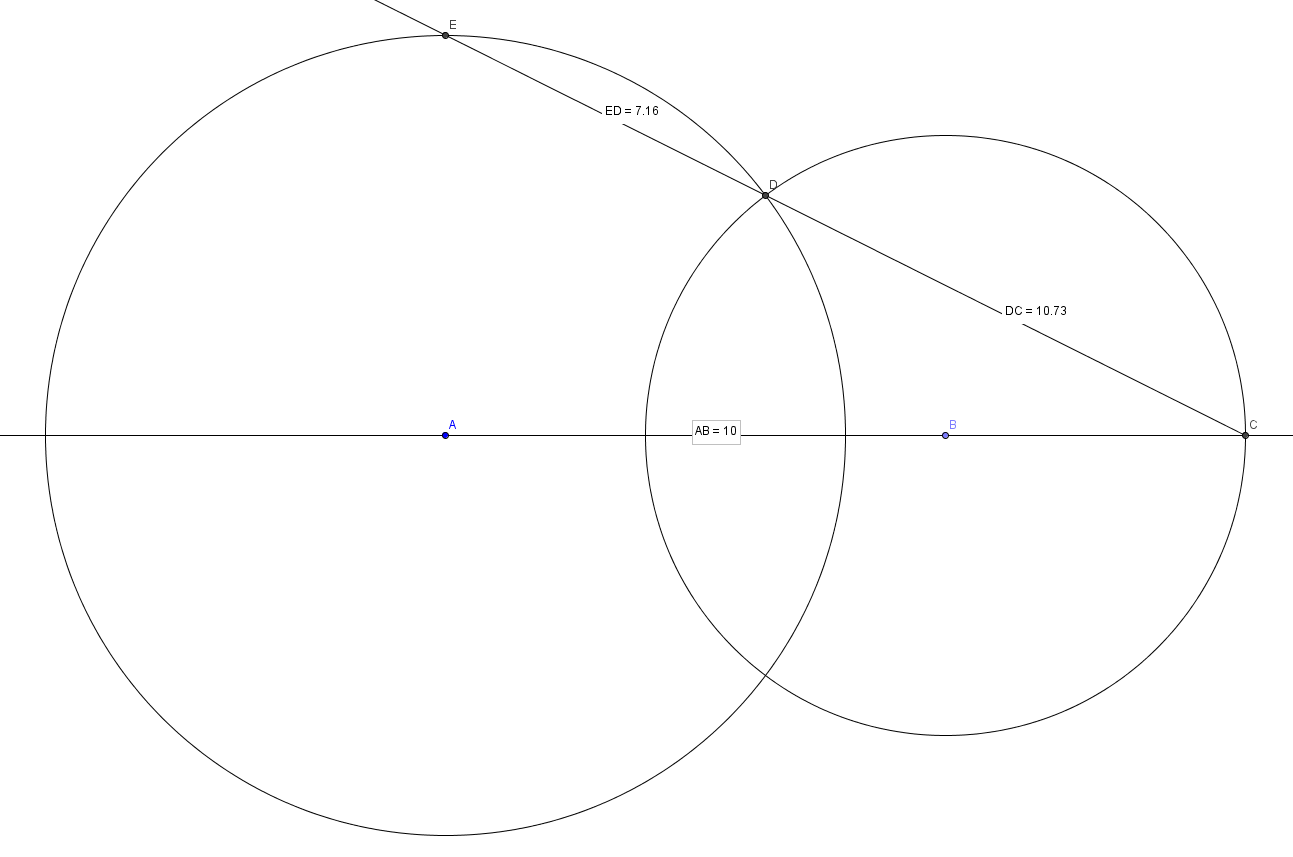
- ab)10.png (37.56 KiB) Viewed 1715 times
Så det jeg lurer på er hvordan en kan gå fram for å vise at at den forlengede linjen mellom sentrene treffer R på sirkelbuen, gitt betingelsene i oppgaveteksten.
Re: Geometri-problemløsing
Posted: 29/04-2015 22:03
by Lektorn
Du kan vel vise at det blir to kongruente trekanter her. Hvis du kaller skjæringspunktet mellom AB og den lille sirkelen for F (punktet nærmest A) så vil trekant CDF være kongruent med trekant EDF.

