Page 1 of 1
Er det slik denne oppgaven skal regnes ut?
Posted: 04/05-2015 14:11
by MatteRudabe
Hei!
Jeg driver og regner ut oppgaver knyttet til forkorting av rasjonale uttrykk. Jeg kom over en "regn ut" oppgave. Jeg syns det er noe rart med min regnemåte. Skal man ikke gjøre likt på begge sider av + og - tegnet? eller har jeg gjort det riktig?
legger ved vedlegg over oppgaven.
takk for hjelpen!

- 20150504_140835_HDR~2.jpg (421.69 KiB) Viewed 2162 times
Re: Er det slik denne oppgaven skal regnes ut?
Posted: 04/05-2015 14:16
by Aleks855
Hei!
Ja, dette blir feil pga. måten du forkorter brøken på.
Se her for mer info:
http://udl.no/r1-matematikk/kapittel-1- ... ttrykk-865
Da ser du kanskje hvor ting går galt.
Re: Er det slik denne oppgaven skal regnes ut?
Posted: 04/05-2015 14:19
by MatteRudabe
Glemte å si at fasiten til oppgaven er det jeg fikk som svar. 3x-6.
Re: Er det slik denne oppgaven skal regnes ut?
Posted: 04/05-2015 14:22
by Aleks855
Sånt skjer. I enkelte tilfeller går det ved tilfeldighet.
Det blir det samme som å si at $\sin(x) + \sin(x) = \sin(x)$ fordi $\sin(0) + \sin(0) = \sin(0)$. Den siste likheten er sann.
Re: Er det slik denne oppgaven skal regnes ut?
Posted: 04/05-2015 14:32
by MatteRudabe
Jeg så videoen, og regnet det på nytt. Tror dette blir riktig nå. Legger ved vedlegg over oppgaven jeg regnet ut på nytt.
Takk for hjelpen!
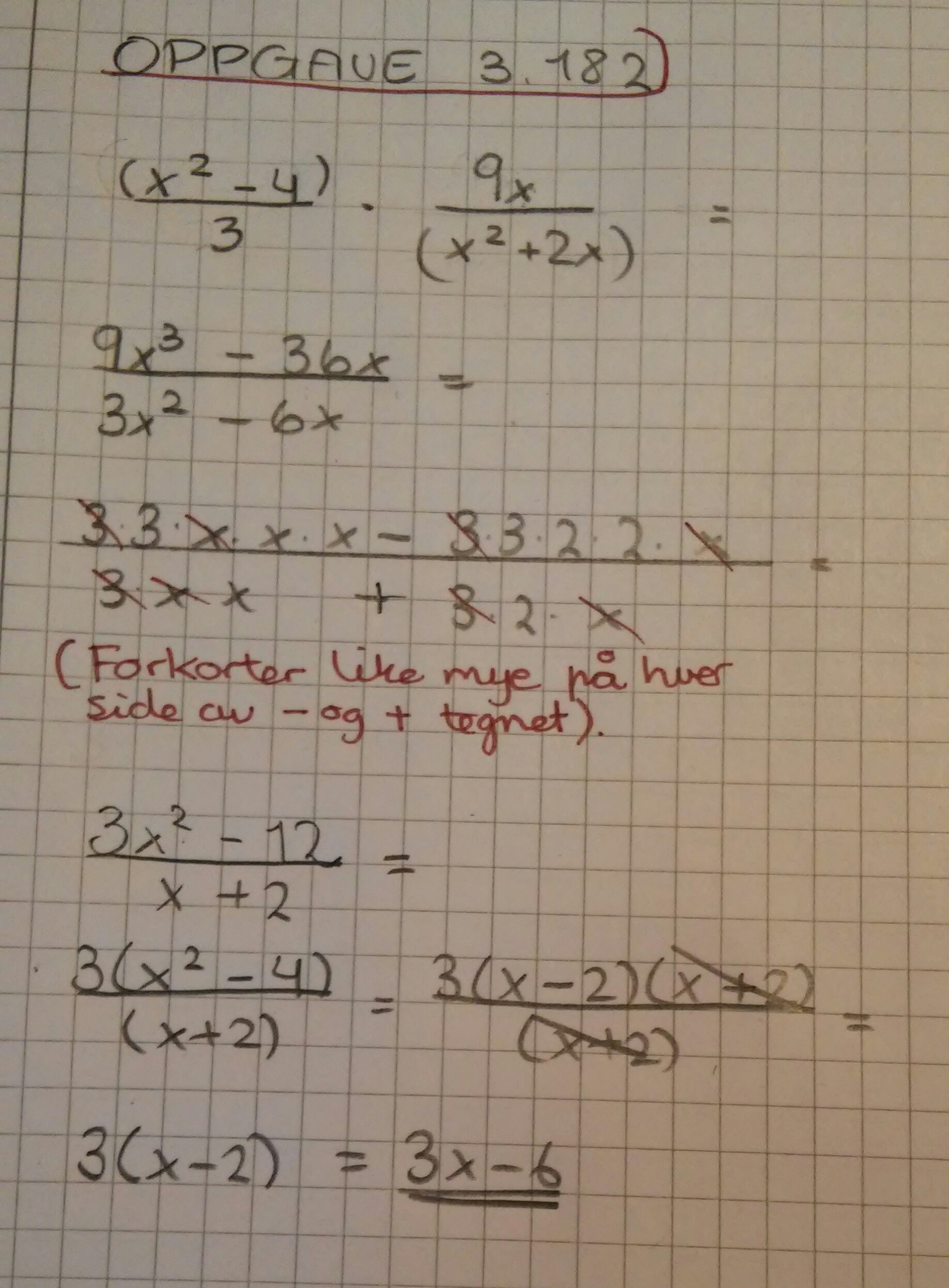
- 20150504_142957_HDR~2.jpg (637.13 KiB) Viewed 2146 times
Re: Er det slik denne oppgaven skal regnes ut?
Posted: 04/05-2015 14:40
by Aleks855
Perfekt!
Et lite tips: En litt mer håndterlig måte å gjøre det på er å faktorisere (som egentlig er det du har gjort, men skrevet på en mer oversiktlig måte). $$\frac{3\cdot3\cdot x \cdot x \cdot x - 3\cdot3\cdot2\cdot2\cdot x}{3\cdot x\cdot x + 3\cdot2\cdot x} = \frac{3x(3x^2 + 12x)}{3x(x+2)} = \frac{\cancel{3x}(3x^2 + 12x)}{\cancel{3x}(x+2)}$$ og derfra fortsette slik du gjorde. Dette med faktorisering er en VELDIG god vane å ha med seg, og er veldig medgjørlig når du allerede har vist at du kan å identifisere felles faktorer. Her kunne vi stryke 3x over og under fordi det hele var faktorisert.
Re: Er det slik denne oppgaven skal regnes ut?
Posted: 04/05-2015 15:10
by Nebuchadnezzar
Eventuelt: Siden $x^2-4=x^2-2^2 = (x-2)(x+2)$ og $x^2+2x = x(x+2)$ så er
$$ \hspace{1cm}
\frac{(x^2-4)}{3} \cdot \frac{9x}{(x^2+2x)}
= \frac{(x-2)(x+2)}{3} \cdot \frac{3 \cdot 3x}{x(x+2)}
= \frac{3x \cdot 3 (x-2)(x+2)}{3x(x+2)}
= 3(x - 2)
$$