Page 1 of 1
Bevis av primtall
Posted: 11/05-2015 14:17
by pi-ra
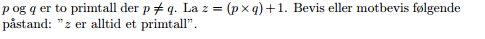
- primtallBevis.PNG (8.39 KiB) Viewed 2061 times
Sliter litt med hvordan jeg skal sette opp dette beviset matematisk. Hvordan representerer jeg f.eks. et primtall generelt for å kunne bruke det videre i utregningen?
Eksamen imorgen, så hadde vært fint med raske svar. Alle innspill er velkomne!

Re: Bevis av primtall
Posted: 11/05-2015 14:32
by Nebuchadnezzar
Enkleste er et motbevis, klarer du å finne to slike primtall p og q slik at $p \cdot q + 1$ ikke er et primtall?
Re: Bevis av primtall
Posted: 11/05-2015 14:46
by pi-ra
p=11 og q=13 gir vel pq+1=144 som er delelig på 2.
Men er litt usikker på om dette holder..? Vi fikk spesifikt vite at det ikke holdt å bevise det for enkelte tall, men at beviset måtte gjelde generelt. Hva gjør man da?
Re: Bevis av primtall
Posted: 11/05-2015 15:15
by Norm
La [tex]z = p \times q + 1[/tex], der [tex]p > q[/tex]. Vi antar at [tex]z[/tex] alltid er et primtall. Tar først tilfellet [tex]q = 2[/tex]. Da har man at [tex]\frac{z - 1}{2}[/tex] alltid er et primtall, og alt er vel. Vi vet at alle primtall [tex]> 2[/tex] er oddetall. Så vi setter inn
[tex]z = (2l + 1)(2k + 1) + 1 = 4lk + 2l + 2k + 2[/tex] og får at [tex]z[/tex] er delelig på 2 for alle [tex]p,q[/tex]. Detter er helt klart en selvmotsigelse, og [tex]z[/tex] kan ikke være et primtall for alle [tex]p,q[/tex].
Re: Bevis av primtall
Posted: 11/05-2015 16:56
by Nebuchadnezzar
Når du skal bevise at noe er sant, må du vise at det holder for alle $p$ og $q$.
Når du skal motbevise noe trenger du bare ETT moteksempel. 2 og 3 ville og fungert siden 6 ikke er et primtall.
Oppgaven spør jo om påstanden holder for alle $p$ og $q$ og ved å finne ett eksempel
hvor det ikke stemmer, så holder jo ikke påstanden og du er ferdig.
Så ofte er det langt enklere å vise at noe ikke holder, enn å vise at noe faktisk stemmer.
