Page 1 of 1
Massesenter
Posted: 24/05-2015 13:29
by pi-ra
- 2010ex2, fysikk.PNG (44.68 KiB) Viewed 2603 times
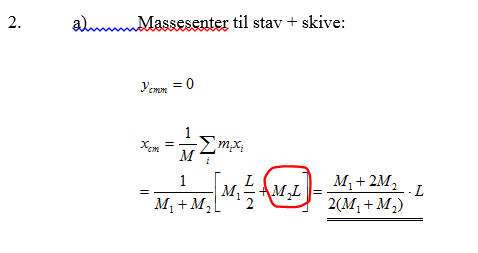
- 2010ex2, fysikk fasit.PNG (6.5 KiB) Viewed 2603 times
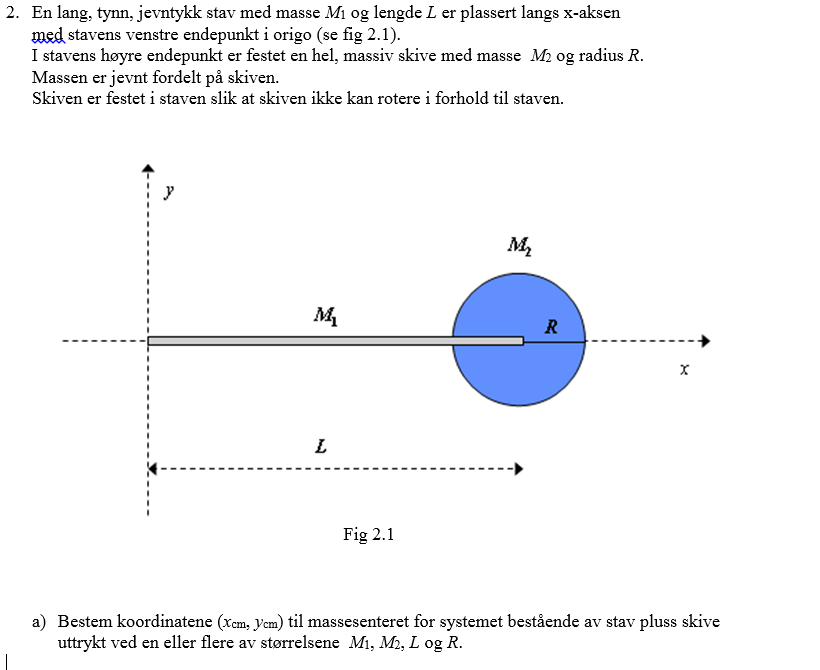
1. I forhold til det som er ringet med rødt: Hvorfor skal det her ganges med L og ikke med R? Formelen sier jo man skal gange massen*radien?
2. Hvorfor er massesenteret for y-koordinaten lik 0?
Re: Massesenter
Posted: 24/05-2015 15:45
by zell
Regn "moment" om x=0. Totalmassen ganget med massesenterets avstand fra x=0 må da være likt masse ganget med arm for de to delene (staven og skiven).
Staven har bidrag [tex]M_1\cdot \frac{L}{2}[/tex]
Skiven har bidrag [tex]M_2\cdot L[/tex]
Altså må: [tex]M\cdot x_{cm} = M_1\frac{L}{2}+M_2L \ \Rightarrow \ x_{cm} = \frac{1}{M_1+M_2}\left[M_1\frac{L}{2}+M_2L\right][/tex]
Du ser at y-koordinaten til massesenteret er i null siden x-aksen deler både staven og skiven langs midten. Hvis du har lyst til å vise det ved regning er det bare å regne "moment" om y=0.
Re: Massesenter
Posted: 24/05-2015 17:03
by pi-ra
Kunne du forklart litt nærmere hvorfor de har det bidraget de har? Skal man ikke se på objektene (staven og skiven) hver for seg hvor skiven vil ha et bidrag M1 * R?
Re: Massesenter
Posted: 24/05-2015 23:40
by zell
Hvis du hadde plassert skiven helt til venstre så ville bidraget blitt det. Tenk på det som to punktmasser, avstanden mellom de to punktmassene vil utvilsomt påvirke tyngepunktets posisjon.
Re: Massesenter
Posted: 24/05-2015 23:53
by pi-ra
zell wrote:Hvis du hadde plassert skiven helt til venstre så ville bidraget blitt det. Tenk på det som to punktmasser, avstanden mellom de to punktmassene vil utvilsomt påvirke tyngepunktets posisjon.
Hmm, stemmer. Når man ser på [tex]r[/tex] for hver av disse punktmassene, skal man da se på lengden/radien frem til senteret av punktmassene? Høres veldig logisk ut hvertfall.
Re: Massesenter
Posted: 25/05-2015 00:02
by zell
Det du i prinsippet gjør er å samle begge punktmassene i én punktmasse med avstand til y-aksen slik at systemet er uendret. Den avstanden finner du ved å si at den samlede massen ganget avstanden til y-aksen, skal være lik de to punktmassene ganget med sine respektive avstander til y-aksen.