matematikk.net

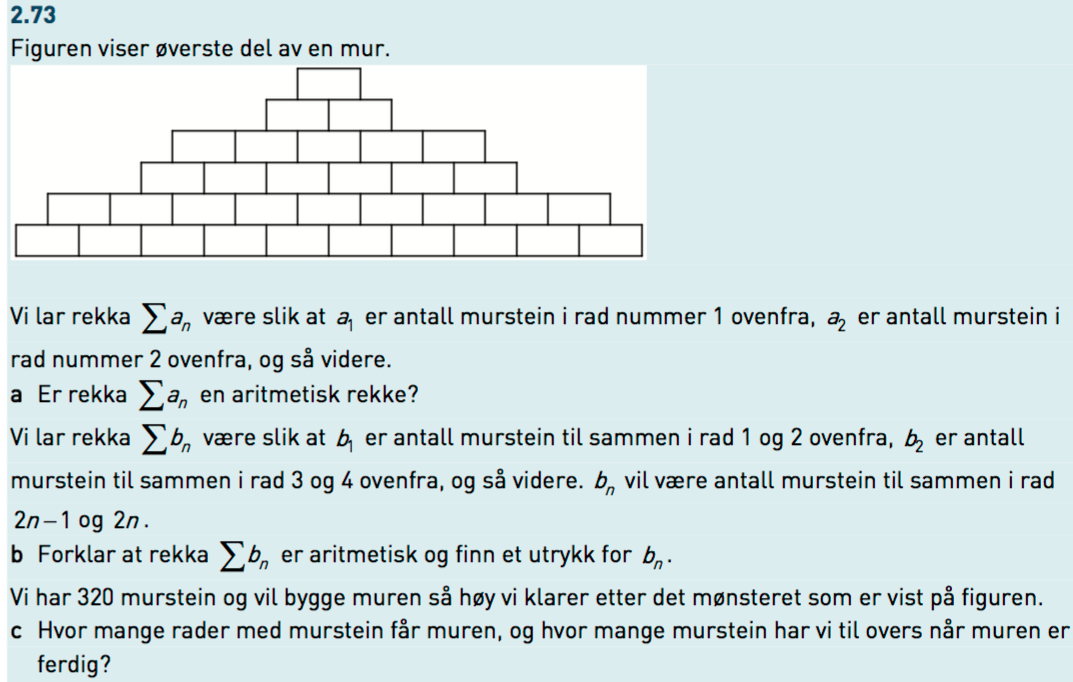
Hei, har en oppgave jeg trenger litt hjelp med. Jeg skjønner hva den går ut på, men sliter litt med c, der man skal finne ut hvor mange rader man kan bygge med 320 steiner, der 2 og 2 rader er aritmetiske. Jeg fikk feil på antall rader, men fikk rett på antall resterende steiner. Oppgaven kan du se under.

Hei, har enda en oppgave jeg lurer litt på.


Atif tar opp et annuitetslån på 1 200 000 kr. Lånet skal betales tilbake med årlige terminbeløp over 15 år. Renten er 5,3 % og første terminbeløp forfaller om ett år.
a Hvablirterminbeløpet?
b På et tidspunkt vinner Atif i tipping, og rett etter betalingen av det 9. terminbeløpet går han i
banken for å innfri lånet. Hva må han betale?

Er da b jeg ikke får til, men jeg tenker da at det blir en geometrisk rekke med åtte ledd og k = 1,053^-1? Terminbeløpet er 117967.

Summen av en aritmetisk rekke er gitt ved [tex]S_n=\dfrac{n\cdot (a_1+a_n)}{2}[/tex] hvor [tex]a_n=a_1+(n-1)d[/tex]
Her er $a_n = b_n$ i oppgaven din (som du fant i b) så da er det bare å sette inn i formelen og løse for n. n er antall rader du får om du legger to og to rader om gangen (som er det vi gjør i oppgave b) så det endelige tallet må du gange med 2. (altså (n/2)) Formelen for $b_n$ har du sikkert fått til å være $b_n=8n-5$. Dette betyr at $b_1=3$, $b_2=11$, $b_3=19$ osv.
Så du får en ny følge: 3, 11, 19 ... Som også er aritmetisk med $d=8$.

Altså har vi: $b_{\frac{n}{2}}=b_1+\left( \left(\frac{n}{2} \right)-1 \right)d$ som gir $S_{\frac{n}{2}}= \dfrac{\left(\frac{n}{2}\right) \cdot \left(b_1+b_{\frac{n}{2}}\right)}{2}\Rightarrow S_{\frac{n}{2}}=\dfrac{\left(\frac{n}{2}\right) \cdot (3 + 8 \left(\frac{n}{2}\right)-5)}{2} = \dfrac{\frac{\cancel{4} \cdot 2n^2}{\cancel{4}}-\frac{\cancel{2}n}{\cancel{2}}}{2} = n^2-\frac{n}{2}$

Problemet vårt nå er at $b_n$ bare fungerer for 2 og 2 rader om gangen så rekken er ikke aritmetisk for et oddetall antall rader og dermed er også formelen ubrukbar for oddetalls n. For å løse dette må vi sette på en liten betingelse. Når n er et oddetall tar vi istedenfor forrige partall og adderer summen av neste oddetalls rekke. La oss f.eks. si at n=3, da bruker vi formelen for n=2 og adderer $\frac{b_{\frac{3+1}{2}}-1}{2}$ til svaret. (for å få summen av den korteste rekka for en vilkårlig $b_n$. Husk også at vi bruker n/2 og ikke n fordi $b_n$ teller 2 og 2 rader)
[tex](n-1)^2-\frac{n-1}{2} + \frac{b_{\frac{n+1}{2}}-1}{2} = (n-1)^2-\frac{n-1}{2} + \frac{8(\frac{n+1}{2})-5-1}{2}[/tex]
[tex]= n^2-2n+1-\frac{n-1}{2}+2(n+1)-3 = n^2 -\frac{(n-1)}{2} + 2(n+1) - 2n - 2 = n^2 - \frac{(n-1)}{2} + 2(n+1) - 2(n+1)[/tex]
[tex]= n^2 - \frac{n-1}{2}[/tex]

\begin{cases}
n^2-\frac{n}{2} & n = 2, 4, 6 ... \\
n^2-\frac{n-1}{2} & n = 1, 3, 5 ... \\
\end{cases}

Dette kan vi omforme til en formel ved å gjøre et lite triks.
[tex]n^2-\frac{\left(n-\frac{1}{2} + (-1)^{n+1} \cdot \frac{1}{2} \right)}{2} = n^2-\frac{\left(n-\frac{1}{2}\left(1+(-1)^{n+1}\right)\right)}{2}[/tex]
[tex]=n^2+\frac{\left(1+(-1)^{n+1}\right) - 2n}{4}[/tex]

Her har jeg delt opp 1 i to halve og satt på en test som vil slå ut begge deler om n er et partall (slik at uttrykket blir $2n^2-)(n-1)$) eller slå dem sammen for å få den opprinnelige ligningen ($2n^2-n$) vår om n skulle være et partall.

Om det nå blir et desimaltall runder du bare ned til nærmeste heltall og utnytter at $S_x - S_{n} = x$ for å finne resterende antall steiner.

Eksempel (20 steiner):
[tex]n^2+\frac{1+(-1)^{n+1}-2n}{4}=20 \Rightarrow n \approx 4.69 \Rightarrow n=4[/tex]
[tex]20 - S_4 = x \Leftrightarrow 20-\left((4)^2+\frac{1+(-1)^{(4)+1}-2(4)}{4}\right) = x \Leftrightarrow x=6[/tex]
Det er altså 4 rader med stein og 6 stein til overs når vi starter med 20 stein.

Er det et sted du falt av så er det bare å si ifra så skal jeg prøve å forklare på nytt. Det ble jo ikke akkurat noe smooth løsning, men det er nå i alle fall et akseptabelt svar. Jeg kan ikke fatte og forstå at dette skal være rekker i S2 med mindre det er noe alvorlig jeg har gått glipp av i løpet av videregående matten.