Page 1 of 1
Vertikal glider for å finne overskudd
Posted: 24/11-2015 12:59
by rawrstad
Hei! Noen som vet hvordan man finner ut når overskuddet er størst av en produksjon av en vare i geogebra? Altså, uten å regne ut en formel for O(x) først. Man skal bare finne ut hvor den vertikale avstanden mellom I(x) og K(x) er størst. Har et bilde av det men vet ikke hvordan det legges inn..
Re: Vertikal glider for å finne overskudd
Posted: 24/11-2015 14:07
by Dolandyret
rawrstad wrote:Hei! Noen som vet hvordan man finner ut når overskuddet er størst av en produksjon av en vare i geogebra? Altså, uten å regne ut en formel for O(x) først. Man skal bare finne ut hvor den vertikale avstanden mellom I(x) og K(x) er størst. Har et bilde av det men vet ikke hvordan det legges inn..
Snakk om P-matte eksamen? Da har du 2 grafer, Inntekt(x) og Kostnad(x). Vi har definisjonen: Overskudd=Inntekt-Kostnad.
Lag derfor en graf Overskudd(x)=Inntekt(x)-Kostnad(x). Da finner du at overskuddet er størst ved produksjon av 45 varer, og da vil overskuddet være 5312,50Kr.
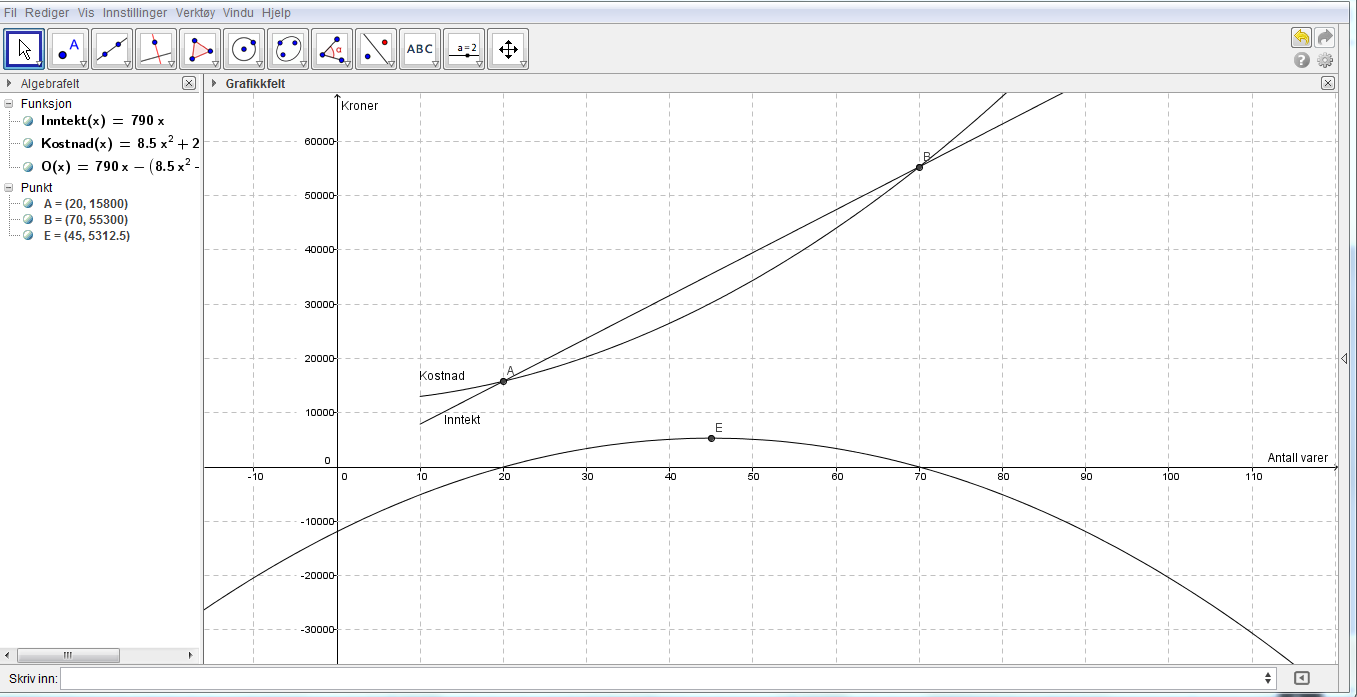
- Oppgave 1.png (77.66 KiB) Viewed 3074 times
Re: Vertikal glider for å finne overskudd
Posted: 24/11-2015 15:23
by rawrstad
Dolandyret wrote:rawrstad wrote:Hei! Noen som vet hvordan man finner ut når overskuddet er størst av en produksjon av en vare i geogebra? Altså, uten å regne ut en formel for O(x) først. Man skal bare finne ut hvor den vertikale avstanden mellom I(x) og K(x) er størst. Har et bilde av det men vet ikke hvordan det legges inn..
Snakk om P-matte eksamen? Da har du 2 grafer, Inntekt(x) og Kostnad(x). Vi har definisjonen: Overskudd=Inntekt-Kostnad.
Lag derfor en graf Overskudd(x)=Inntekt(x)-Kostnad(x). Da finner du at overskuddet er størst ved produksjon av 45 varer, og da vil overskuddet være 5312,50Kr.
Oppgave%201.png
Nei det er S1 det er snakk om her. Eksamen høsten 2010 del 2, oppgave 6, alternativ II c).
Bruk grafene til å avgjøre hvor mye som må produseres for at bedriften skal sitte igjen
med overskudd. Forklar hvordan du kan bruke grafene til å finne det største
overskuddet.
I fasiten hade de laget en vertikal glider som fant overskuddet (den største avstanden mellom I(x) og K(x), uten å bruke en formel for O(x).
Re: Vertikal glider for å finne overskudd
Posted: 24/11-2015 15:34
by Kjemikern
Trykk på funksjonen glider. Plasser den et sted. Høyreklikk og trykk på egenskaper. Endre standardintervallene [-5,5] til det som er naturlig for funksjonen f.eks. [0,2000]
Kall differansen mellom inntekt og kostnad for O, Skriv så i algebrafeltet. O=I(a)-k(a).
Da vil du sa at O endrer seg når du drar på glideren.
Det du gjør er egentlig å lage deg en ny funksjon uttrykt med variabelen a istedenfor x. Jeg vil anta det er enklere å heller gjøre den må den "gamle" måten.
O(x)=I(x)-K(x), også bruke funksjonen ekstremalpunkt. Da slipper du å tegne glidere o.l. men til slutt er det opp til hva personen synes er enklest å gjøre

Re: Vertikal glider for å finne overskudd
Posted: 24/11-2015 15:58
by rawrstad
Kjemikern wrote:Trykk på funksjonen glider. Plasser den et sted. Høyreklikk og trykk på egenskaper. Endre standardintervallene [-5,5] til det som er naturlig for funksjonen f.eks. [0,2000]
Kall differansen mellom inntekt og kostnad for O, Skriv så i algebrafeltet. O=I(a)-k(a).
Da vil du sa at O endrer seg når du drar på glideren.
Det du gjør er egentlig å lage deg en ny funksjon uttrykt med variabelen a istedenfor x. Jeg vil anta det er enklere å heller gjøre den må den "gamle" måten.
O(x)=I(x)-K(x), også bruke funksjonen ekstremalpunkt. Da slipper du å tegne glidere o.l. men til slutt er det opp til hva personen synes er enklest å gjøre

Tusen takk

Ja det er mye enklere på den vanlige måten.. Jeg bare lurte på om de oppgaven krevde noe mer enn å forklare at der avstanden er størst mellom I(x) og K(x), finner vi det største overskuddet. Regner det jo ut med formelen for O(x) i neste deloppgave.