matematikk.net

Eksempeloppgave S1 2014, del 2, oppgave 1 (http://matematikk.net/res/eksamen/S1/S1 ... sempel.pdf)

Et rett prisme har sidene a, b og c. Volumet er 200, diagonalen d (inne i prismet) er
141 og overflaten er 220.
Vis at vi kan stille opp følgende likningssystem utfra opplysningene om prismet.
II: a^2+b^2+c^2=d^2


Fasiten sier at man tar pytagoras to ganger.

Er det noen som kan forklare litt grundigere?

Gjest wrote:Eksempeloppgave S1 2014, del 2, oppgave 1 (http://matematikk.net/res/eksamen/S1/S1 ... sempel.pdf)

Et rett prisme har sidene a, b og c. Volumet er 200, diagonalen d (inne i prismet) er
141 og overflaten er 220.
Vis at vi kan stille opp følgende likningssystem utfra opplysningene om prismet.
II: a^2+b^2+c^2=d^2


Fasiten sier at man tar pytagoras to ganger.

Er det noen som kan forklare litt grundigere?

Skal prøve så godt jeg kan :p

Pytagoras' setning forteller oss at: [tex]Hypotenus^2=Katet_{1}^{2}+Katet_{2}^{2}[/tex]

Først har vi [tex]a^2+b^2[/tex]. [tex]a[/tex] og [tex]b[/tex] er de 2 katetene i de to rettvinklede trekantene vi får om vi deler grunnflaten diagonalt. Vi får diagonalen i grunnflaten ved å ta [tex]\sqrt{a^2+b^2}[/tex].

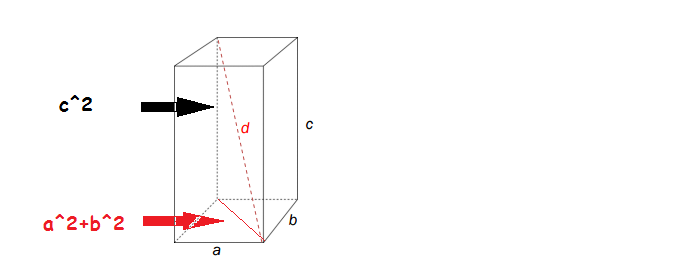
Så har vi at [tex](a^2+b^2)+c^2=d^2[/tex]. Se nå for deg at i det øverste hjørnet hvor diagonalen [tex]d[/tex] "begynner", så har vi høyden [tex]c[/tex] ned på diagonalen vi uttrykker ved [tex]\sqrt{a^2+b^2}[/tex].

[tex]d[/tex] blir derfor lengden av hypotenusen i uttrykket [tex]\sqrt{(a^2+b^2)}+c[/tex].

Edit: Jeg vet at [tex]a^2+b^2[/tex] og [tex]c^2[/tex] ikke er de korrekte lengdene av katetene i illustrasjonen under, men at kvadratroten av de er det. De ble bare brukt for å få frem budskapet enklest mulig.

Klarer du å tegne en rettvinklet trekant der hypotenusen er diagonalen i prismet?

Dolandyret wrote:

Gjest wrote:Eksempeloppgave S1 2014, del 2, oppgave 1 (http://matematikk.net/res/eksamen/S1/S1 ... sempel.pdf)

Et rett prisme har sidene a, b og c. Volumet er 200, diagonalen d (inne i prismet) er
141 og overflaten er 220.
Vis at vi kan stille opp følgende likningssystem utfra opplysningene om prismet.
II: a^2+b^2+c^2=d^2


Fasiten sier at man tar pytagoras to ganger.

Er det noen som kan forklare litt grundigere?

Skal prøve så godt jeg kan :p


Pytagoras' setning forteller oss at: [tex]Hypotenus^2=Katet_{1}^{2}+Katet_{2}^{2}[/tex]

(Skal prøve å illustrere etterpå).

Først har vi [tex]a^2+b^2[/tex]. Disse er da de 2 katetene i de to rettvinklede trekantene vi får om vi deler grunnflaten diagonalt. Vi får diagonalen i grunnflaten ved å ta a^2+b^2.

Så har vi at [tex](a^2+b^2)+c^2=d^2[/tex]. Se nå for deg at i det øverste hjørnet hvor diagonalen [tex]d[/tex] "begynner", så har vi høyden [tex]c[/tex] ned på diagonalen vi uttrykker ved [tex]a^2+b^2[/tex].

d blir derfor lengden av hypotenusen i uttrykket [tex](a^2+b^2)+c^2[/tex].

Tusen takk, skal se om jeg skjønner dette

Gjest wrote:

Dolandyret wrote:

Gjest wrote:Eksempeloppgave S1 2014, del 2, oppgave 1 (http://matematikk.net/res/eksamen/S1/S1 ... sempel.pdf)

Et rett prisme har sidene a, b og c. Volumet er 200, diagonalen d (inne i prismet) er
141 og overflaten er 220.
Vis at vi kan stille opp følgende likningssystem utfra opplysningene om prismet.
II: a^2+b^2+c^2=d^2


Fasiten sier at man tar pytagoras to ganger.

Er det noen som kan forklare litt grundigere?

Skal prøve så godt jeg kan :p


Pytagoras' setning forteller oss at: [tex]Hypotenus^2=Katet_{1}^{2}+Katet_{2}^{2}[/tex]

(Skal prøve å illustrere etterpå).

Først har vi [tex]a^2+b^2[/tex]. Disse er da de 2 katetene i de to rettvinklede trekantene vi får om vi deler grunnflaten diagonalt. Vi får diagonalen i grunnflaten ved å ta a^2+b^2.

Så har vi at [tex](a^2+b^2)+c^2=d^2[/tex]. Se nå for deg at i det øverste hjørnet hvor diagonalen [tex]d[/tex] "begynner", så har vi høyden [tex]c[/tex] ned på diagonalen vi uttrykker ved [tex]a^2+b^2[/tex].

d blir derfor lengden av hypotenusen i uttrykket [tex](a^2+b^2)+c^2[/tex].

Tusen takk, skal se om jeg skjønner dette

Slang med en illustrasjon nå

Slang med en illustrasjon nå [/quote]


Det er c^2 jeg ikke helt skjønner. Hvor kan du legge til denne?

Gjest wrote:Det er c^2 jeg ikke helt skjønner. Hvor kan du legge til denne?

Om du ser for deg at [tex]d[/tex] er hypotenusen i en rettvinklet trekant, så er den ene kateten i denne trekanten [tex]\sqrt{a^2+b^2}[/tex] og den andre kateten blir da høyden av prismet som er [tex]c[/tex]

Dolandyret wrote:

Gjest wrote:Det er c^2 jeg ikke helt skjønner. Hvor kan du legge til denne?

Om du ser for deg at [tex]d[/tex] er diagonalen i en rettvinklet trekant, så er den ene kateten i denne trekanten [tex]a^2+b^2[/tex] og den andre kateten blir da høyden av prismet som er [tex]c^2[/tex]

aah! Nå ser jeg det! Tusen takk Nok matte for i kveld kanskje, haha

Et forslag:

Ups! Skal stå d^2