Page 1 of 1
Potenslikning
Posted: 01/12-2015 18:49
by Guest
Hei, jeg kom over en oppgave jeg synes var vanskelig:
x^(x-1)=6561
Jeg tenkte at jeg kunne bruke logaritmer:
x-1lgx=lg6561
Etter at jeg hadde gjort det her ble jeg plutselig usikker, noen som har tips eventuelt løsning til oppgaven?
Re: Potenslikning
Posted: 01/12-2015 20:29
by Dolandyret
Gjest wrote:Hei, jeg kom over en oppgave jeg synes var vanskelig:
x^(x-1)=6561
Jeg tenkte at jeg kunne bruke logaritmer:
x-1lgx=lg6561
Etter at jeg hadde gjort det her ble jeg plutselig usikker, noen som har tips eventuelt løsning til oppgaven?
Hmm, vet ikke helt hvordan denne skal løses, men jeg løste den i wolfram og fikk:
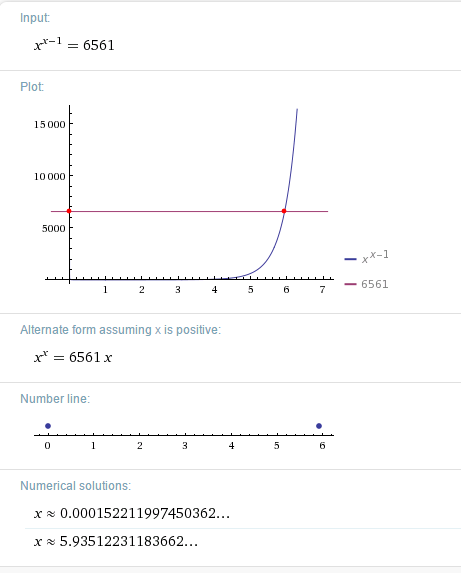
- 6561.png (14.44 KiB) Viewed 2440 times
Re: Potenslikning
Posted: 01/12-2015 22:59
by Fysikkmann97
x = 5,94035 ?
Re: Potenslikning
Posted: 01/12-2015 23:37
by Dolandyret
Fysikkmann97 wrote:x = 5,94035 ?
x=5,9351. Nesten tho. Hvordan kom du fram til det?
Re: Potenslikning
Posted: 01/12-2015 23:54
by Fysikkmann97
Prøv og feil

Eksponenten er jo ett tall lavere enn grunntallet så var det jo bare å finne rett verdi.
Re: Potenslikning
Posted: 02/12-2015 10:03
by Kjellxyz
2 løsninger!
Re: Potenslikning
Posted: 02/12-2015 10:48
by Janhaa
Mulig å løse denne med Lamberts Omega funksjon, mon tro?
Re: Potenslikning
Posted: 02/12-2015 11:41
by Nebuchadnezzar
Janhaa wrote:Mulig å løse denne med Lamberts Omega funksjon, mon tro?
Nei den negative potenser ødelegger dessverre! Men taylorutvikling gir gode resulter
$
-{\frac {36}{7}}\,\log \left( 6 \right) +{\frac {12}{7}}+6/7\,\sqrt {
36\, \left( \log \left( 6 \right) \right) ^{2}-10\,\ln \left( 6
\right) +112\,\log \left( 3 \right) +25}
$
Evt kan en alltids bare bruke newtons tilnærmingsmetode.