Page 1 of 1
krefter
Posted: 10/12-2015 18:01
by Guest
Hei, kan noen hjelpe meg. Jeg er fullstendig blank. :-/
En kraft på 18 N skal deles i to komponenter som står
normalt på hverandre. Den ene komponenten skal
danne en vinkel på 60° med kraften.
Tegn figur og beregn komponentene.
Re: krefter
Posted: 10/12-2015 22:52
by NOGJ
Heisann!
Tenk på en rettvinklet trekant der hypotenusen er kraften din(18N). De to andre kreftene, la oss kalle dem Fx og Fy, danner da hosliggende katet og motstående katet.
Du vet også at en av komponentene vil danne en vinkel på 60 grader til din opprinnelige kraft.
Så da er det bare å kjøre på med litt trigonometri

Re: krefter
Posted: 10/12-2015 22:56
by Dolandyret
Gjest wrote:Hei, kan noen hjelpe meg. Jeg er fullstendig blank. :-/
En kraft på 18 N skal deles i to komponenter som står
normalt på hverandre. Den ene komponenten skal
danne en vinkel på 60° med kraften.
Tegn figur og beregn komponentene.
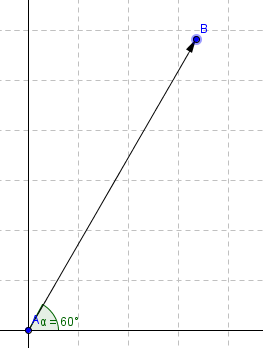
- Dekomponering av 18N.png (6.86 KiB) Viewed 3212 times
Vi dekomponerer en kraft på enklest måte med trigonometri. Se for deg at vektoren som her går fra punkt A til punkt B tilsvarer 18N. Dette kan vi skrive som [tex]F[/tex].
Vi kan dekomponere [tex]F[/tex] og få en kraft i x-retning [tex]F_{x}[/tex] og en kraft i y-retning [tex]F_{y}[/tex]. Summen av disse kreftene skal bli [tex]F[/tex].
[tex]F=F_{x}+F_{y}[/tex]
Her har vi satt at vinkelen [tex]\alpha=60^o[/tex] er vinkelen mellom [tex]F[/tex] og x-aksen. Det vi vil er å finne lengden av vektorene [tex]F_{x}[/tex] og [tex]F_{y}[/tex]. Se for deg at [tex]F[/tex] er hypotenusen i en rettvinklet trekant. For å finne [tex]F_{x}[/tex] har vi: [tex]F_{x}=F*cos(60)=9[/tex]. For å finne [tex]F_{y}[/tex] har vi: [tex]F_{y}=F*sin(60)=9*\sqrt3[/tex].
[tex]F_{y}=9\sqrt3[/tex]
[tex]F_{x}=9[/tex]
Så kan vi tenke pytagoras for å sjekke om svarene er riktige.
[tex]Hypotenus^2=Katet_{1}^2+Katet_{2}^2[/tex]
[tex]18^2=9^2+(9\sqrt3)^2[/tex]
[tex]18^2=324[/tex]
[tex]324=324[/tex]
Re: krefter
Posted: 10/12-2015 23:38
by Guest
Tusen takk begge to
