Page 1 of 1
Geometri nøtteoppgave
Posted: 14/01-2016 18:46
by hdadad
en likesidet trekant er innskrevet i en sirkel. Trekanten har sidelengder lik 8cm. Regn ut radius i sirkelen-
Re: Geometri nøtteoppgave
Posted: 14/01-2016 19:08
by Dolandyret
hdadad wrote:en likesidet trekant er innskrevet i en sirkel. Trekanten har sidelengder lik 8cm. Regn ut radius i sirkelen-
Radius for den omskrevne sirkelen er gitt ved: [tex]r=\frac{abc}{4T}[/tex] hvor T er trekantens areal og abc er sidelengdene. Heron's formel sier at [tex]T=\sqrt{s(s-a)(s-b)(s-c)}[/tex] hvor s er halve sirkelens omkrets, altså summen av sidelengdene delt på 2.
[tex]s=\frac{24}{2}=12[/tex]
[tex]T=\sqrt{12*4*4*4}=\sqrt{768}=27,7128...[/tex]
Fyller inn i formelen og finner at radius i sirkelen er [tex]r=\frac{8^3}{4*27,7128}\approx 4,619[/tex]
Re: Geometri nøtteoppgave
Posted: 14/01-2016 19:13
by Stringselings
Alternativt kan denne løses ved å bruke pytagoras på 2 forskjellige trekanter
Re: Geometri nøtteoppgave
Posted: 14/01-2016 19:16
by fsafafas
Kan du vise?
Re: Geometri nøtteoppgave
Posted: 14/01-2016 19:29
by Stringselings
fsafafas wrote:Kan du vise?
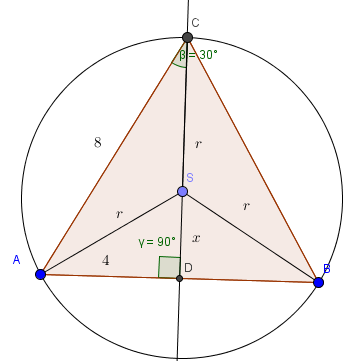
- geo.png (20.11 KiB) Viewed 1885 times
1: [tex]4^2+(x+r)^2=8^2[/tex]
2: [tex]4^2+x^2=r^2[/tex]
Fra 1: [tex]4^2+x^2+2rx+r^2=8^2[/tex]
[tex]r^2+2rx+r^2=8^2[/tex]
[tex]2r(r+x)=8^2[/tex]
[tex]2r \sqrt{8^2-4^2}=8^2[/tex]
[tex]r=8\sqrt3 /3[/tex]