Page 1 of 1
Fortegnslinje for den deriverte
Posted: 08/03-2016 15:10
by sheriff
Hei
Har kommet til kapittel 6.8 i Sinus 1 boka og sliter litt med ett eksempel som er gitt. Har tatt bilde av det istedenfor å skrive inn alt. Det jeg lurer på er hvordan man vet at fortegnslinjen "stiger" først og deretter "synker" for den deriverte av T. Jeg mener, det er ikke noen utregning på det så jeg antar at man bare vet det på grunn av noe, men jeg skjønner ikke hvorfor - det kunne jo vært motsatt også, at den "synker" først og deretter "stiger"? Jeg skjønner at maksimalpunktet er 14 men er ikke helt med på hvordan man vet at den skifter fortegn og "retningen" på kurven.

- IMG_1097.JPG (1.75 MiB) Viewed 3356 times
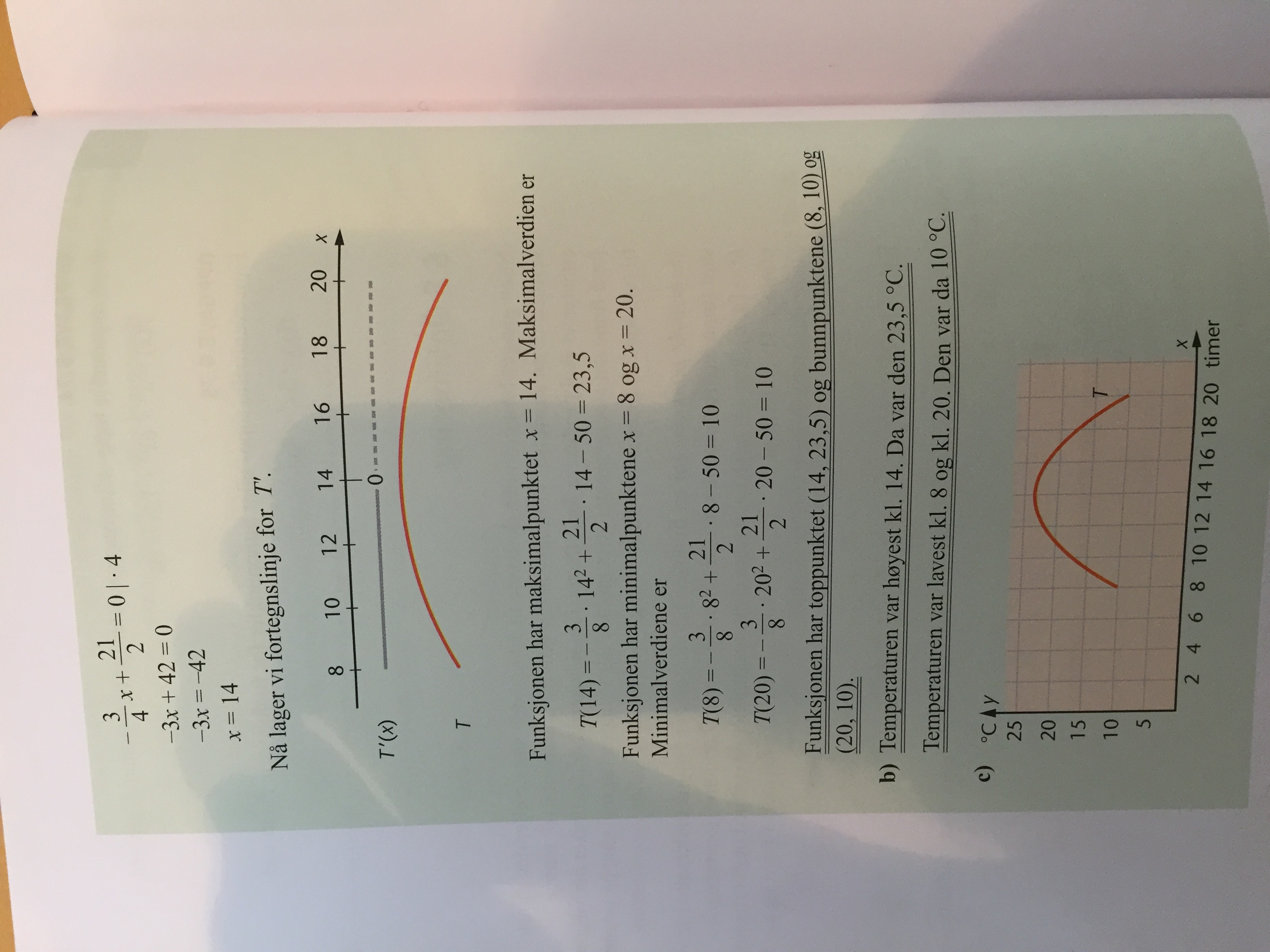
- IMG_1098.JPG (1.58 MiB) Viewed 3356 times
Re: Fortegnslinje for den deriverte
Posted: 08/03-2016 15:21
by madfro
Hei,
Fortegnslinjen viser fortegnet til [tex]T'(x)[/tex].
Så vidt jeg ser er utrykket for den deriverte gitt som
[tex]T'(x) = -\frac{3}{4}x + \frac{21}{2}[/tex].
Som du skriver er nullpunktet til dette utrykket lik 14. Dersom du setter inn en verdi for x som er mindre en 14 vil du få [tex]T'(x < 14) > 0[/tex], mens [tex]T'(x > 14) < 0[/tex].
Når den deriverte er positiv stiger funksjonen, mens den synker nå den deriverte er negativ.
Re: Fortegnslinje for den deriverte
Posted: 08/03-2016 15:30
by sheriff
madfro wrote:Hei,
Fortegnslinjen viser fortegnet til [tex]T'(x)[/tex].
Så vidt jeg ser er utrykket for den deriverte gitt som
[tex]T'(x) = -\frac{3}{4}x + \frac{21}{2}[/tex].
Som du skriver er nullpunktet til dette utrykket lik 14. Dersom du setter inn en verdi for x som er mindre en 14 vil du få [tex]T'(x < 14) > 0[/tex], mens [tex]T'(x > 14) < 0[/tex].
Når den deriverte er positiv stiger funksjonen, mens den synker nå den deriverte er negativ.
Hei, takk for svar. I eksempelet så er det ikke satt inn noen andre verdier enn 14, men betyr det at de som har lagd oppgaven har testet med verdier større og mindre enn 14 for å se om den stiger/synker på henholdsvis venstre og høyre side av nullpunktet? Eller er det en annen smart måte å gjøre det på?
Re: Fortegnslinje for den deriverte
Posted: 08/03-2016 15:41
by madfro
Det du kan gjøre er å skrive om utrykket litt. Siden vi vet at x = 14 er et nullpunkt for den deriverte funksjonen kan vi faktorisere utrykket med [tex](x-14)[/tex] som en faktor.
Her ser vi at vi kan skrive om utrykket slik:
[tex]T'(x) = -\frac{3}{4}(x-14)[/tex]
For dette utrykket kan du nå tegne et nytt fortegnsskjema.
Vi får en linje for faktoren "[tex]-\frac{3}{4}[/tex]" som alltid er negativ, og en linje for faktoren "[tex](x-14)[/tex]" som er positv når [tex]x>14[/tex] og negativ for [tex]x < 14[/tex] (og null for x = 14).
Disse to likningene legges så sammen til en fortegnslinje for hele skjemaet.
Siden den første linjen er negativ hele veien, finner man resultatet ved å bytte rundt på positiv og negativ på den andre linjen.
Re: Fortegnslinje for den deriverte
Posted: 08/03-2016 16:01
by sheriff
madfro wrote:Det du kan gjøre er å skrive om utrykket litt. Siden vi vet at x = 14 er et nullpunkt for den deriverte funksjonen kan vi faktorisere utrykket med [tex](x-14)[/tex] som en faktor.
Her ser vi at vi kan skrive om utrykket slik:
[tex]T'(x) = -\frac{3}{4}(x-14)[/tex]
For dette utrykket kan du nå tegne et nytt fortegnsskjema.
Vi får en linje for faktoren "[tex]-\frac{3}{4}[/tex]" som alltid er negativ, og en linje for faktoren "[tex](x-14)[/tex]" som er positv når [tex]x>14[/tex] og negativ for [tex]x < 14[/tex] (og null for x = 14).
Disse to likningene legges så sammen til en fortegnslinje for hele skjemaet.
Siden den første linjen er negativ hele veien, finner man resultatet ved å bytte rundt på positiv og negativ på den andre linjen.
Sweeet, takk skal du ha. Så det er ett alternativ til å teste med noen verdier for X da?
Re: Fortegnslinje for den deriverte
Posted: 08/03-2016 16:12
by madfro
Dette er nok den beste måten å gjøre det på ja.
Dersom du har et utrykk med flere faktorer, f.eks. et andregradsutrykk så vil du kunne bruke akkurat samme metode.
Re: Fortegnslinje for den deriverte
Posted: 08/03-2016 16:36
by sheriff
madfro wrote:Dette er nok den beste måten å gjøre det på ja.
Dersom du har et utrykk med flere faktorer, f.eks. et andregradsutrykk så vil du kunne bruke akkurat samme metode.
Takk skal du ha
