matematikk.net

Hei

Jeg sitter fast på denne oppgaven, trenger hjelp til å løse denne:

La Y være en poissonvariabel med λt = 5.
Regn ut P(Y = 0), P(2 ≤ Y ≤ 10) og P(Y > 2).

steinein wrote:Hei

Jeg sitter fast på denne oppgaven, trenger hjelp til å løse denne:

La Y være en poissonvariabel med λt = 5.
Regn ut P(Y = 0), P(2 ≤ Y ≤ 10) og P(Y > 2).

Jeg vil gjerne vite metoden, jeg tror svaret på den første skal bli 0,0067. Er det riktig?

[tex]P(Y=0) = \frac{(\lambda t)^0\cdot\mathrm{e}^{-\lambda t}}{0!} = \mathrm{e}^{-5} = 0.0067[/tex]

[tex]P(2\leq Y \leq 10) = P(Y\leq 10) - P(Y\leq 1) = \sum_{i=2}^{10} P(Y=i)[/tex] (her kan du gjøre summeringen selv, eller slå opp i tabell)

[tex]P(Y>2) = 1-P(Y\leq 2) = 1- \left(P(Y=2)+P(Y=1)+P(Y=0)\right)[/tex]

Hei! Hadde et spørsmål, jeg driver og leser litt på en eksamen hvor oppgaven lyder: En variabel X er Poisson fordelt med parameter [tex]\lambda =4[/tex]. Hva er sannsynligheten for X=4 ? (og noen par andre sannsynligheter)

Skjønner ikke helt hvordan jeg skal finne f.eks. X=4 dersom jeg ikke vet hva "t" er?

Se her: https://en.wikipedia.org/wiki/Poisson_distribution

Så det er denne jeg skal bruke, dersom jeg ikke vet hva t er?



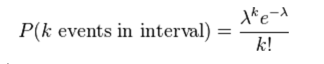
fordi den jeg som oftest pleier å bruke er [tex]\frac{(\lambda t)^{x}}{x!}*e^{-\lambda t}[/tex]

Ja

Tusen hjertelig takk! Da fungerte det!