matematikk.net

Du skal kjøpe en leilighet til 2 500 000 kroner. Du har ingen oppsparte midler og må derfor
låne hele beløpet. Lånet er et annuitetslån med 25 faste årlige tilbakebetalinger der første
tilbakebetaling er om ett år. Den årlige renten på lånet er 2.3 %.
a) Hvor mye blir den faste årlige tilbakebetalingen?
b) Hvor mye er renter og hvor mye er avdrag i den første tilbakebetalingen?
Like etter at du har betalt den 10. tilbakebetalingen, arver du 850 000 kroner. Du bestemmer
deg for å redusere lånet med hele beløpet du arvet.
c) Hvor mye blir nå hver av de siste 15 faste årlige tilbakebetalingene?
___

Forstår virkelig ikke oppgave C. Noen innspill?

Mine tanker:

1. Finn hvor mye rente som er betalt inn.
2. Ta totalt beløp betalt inn minus renter.
3. Trekk fra det beløpet på det han må betale, samt de 850 tusen.

a)

$n = 25$
$S = 2,5 * 10^6$
$a_1 = \frac xk$
$k = 1.023^{-1}$

Denne informasjonen gir da følgende likning vha. sumformelen for geometrisk rekke:

$2,5 * 10^6 = \frac {x}{1.023} * \frac {1.023^{-25} - 1}{1.023^{-1} - 1}$

Løser i CAS:



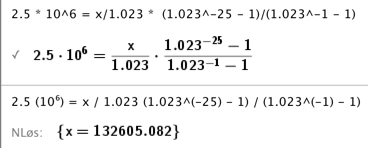
Terminbeløpet blir derfor 132605 kr.


c)

Terminbeløpet er 132605 kr. Setter opp ett "nytt" lån, med femten terminer og samme terminbeløp. Merk at jeg i denne oppgaven har valgt å bruke nåverdien av beløpet. Så den summen jeg kommer frem til, vil være det beløpet som står igjen å betale i dag.

Dette blir da samme betingelser som før, bare at man nå har femten innbetalinger, siden ti av de er overstått.

$S = \frac {132605}{1.023} * \frac {1.023^{-15} - 1}{1.023^{-1} - 1}$ blir da likningen som må løses for å finne beløpet som står igjen å innbetales. Klarer du resten selv?

Merk at jeg bruker at $k = 1.023^{-1}$. Det er det samme som å flytte tallet som er opphøyd under brøkstreken, og få $k = \frac {1}{1.023}$.

Jeg får ikke riktig svar når jeg regner. Irriterende

[tex]2.500.000\frac{1,023^{25}\cdot 0,023}{1,023^{25}-1} = 2.500.000\frac{0,0406}{0,7656} = 132.575,7576\approx 132.576[/tex]

Hva gjør jeg feil?

Ut i fra likningen, så har du satt den opp feil.

Sumformel for geometriske rekker:

S$_n = a_1 * \frac {k^n - 1}{k - 1}$


Nå vet jeg ikke om du prøver å regne med sluttverdi, men jeg vil anbefale å bruke nåverdi på oppgaver som omhandler lån, da du som oftest vil finne nåverdier.

1.Om du vil regne med nåverdi, så er kvotienten feil. Å opphøye den i -1 vil fikse det.
2. Under brøkstreken skal man ikke opphøye i antall terminer, bare over. Over brøkstreken bruker jeg ikke å gange, men å trekke fra 1 da man bare vil finne ut hvor mye rentene har blitt til (siden $0.023^25$ vil gå mot null, bruker vi 1.023 isteden og trekker fra 1 til slutt).

Jeg skjønte desverre ikke

Jeg får det ikke til

hva da?

Jeg forstår ikke hvordan jeg skal regne. Jeg prøver med formelen som står i boka men det blir feil. Jeg vet ikke hvor feilen min ligger.

For geometriske rekker, som annuitetslån er, så kan du bruke denne formelen:


S$_n = a_1 * \frac {k^n - 1}{k - 1}$

$S_n$ er det beløpet som skal betales inn på n år, $a_1$ er terminbeløpet, og vil vanligvis ganges med kvotienten siden første innbetaling er om ett år. Ser du hvorfor det? k er kvotienten, som blir på formen $\frac {1}{1.023}$. n er antall terminer, og da hvor lenge det skal nedbetales. Setter du inn de verdiene som jeg har oppgitt i første posten min, vil du komme frem til rett svar.

Når det gjelder c-oppgaven, så vil du vite hvor mye du har igjen å betale ned på lånet ditt. Der vet du allerede terminbeløpet, og kan da finne restbeløpet ved å endre n fra 25 til 15.

Når jeg regner med de formlene, om det er de dere har lagt eller i boka jeg har så får jeg feil svar. Til og med når jeg regner på eksemplene i boka så blir det feil svar. Begynner å gi opp snart Jeg skal levere denne oppgaven imorgen før kl 09:00. Hvis noen kunne vist med utregning så hadde jeg vært veldig takknemlig