matematikk.net

Hvis Arne Hole bruker vanlig delvis integrasjon i det følgende regnestykket, hvordan har det seg da at han skriver "= -e^x cosx ...", med minus foran e^x:



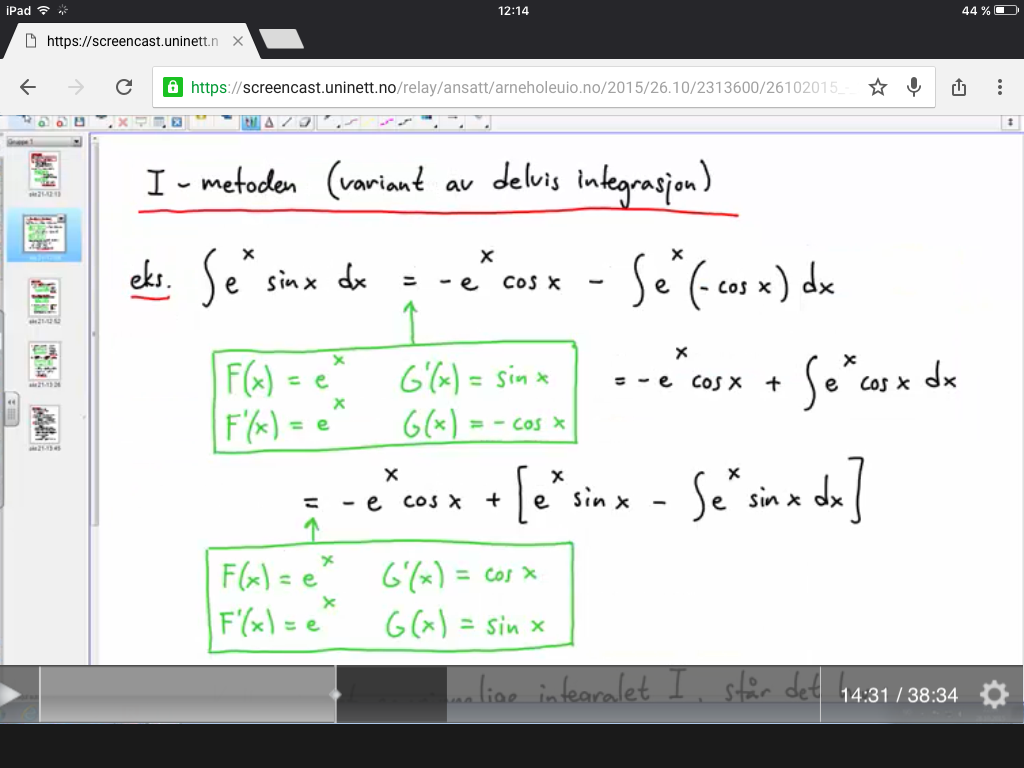https://screencast.uninett.no/relay/ans ... 49_38.html

Btw, har tidligere skrevet her under navnet Anti, så alle som kjenner til mine tidligere innlegg vet at jeg begynte med matte i mars i år, helt fra scratch, så mangel på mengdetrening gjør at jeg foreløpig har noen kunnskapshull her og der. Som newbie vil jeg derfor sette pris på en pedagogisk og trinnvis forklaring på ovennevnte spørsmål.

$F(x) \cdot G(x) = e^x \cdot (-\cos x) = -e^x\cos x$

Minustegnet kommer fra $-\cos x$

Regelen er at $a \cdot (-b) = -ab$

Flott! Antok at han hadde tatt minus-tegnet fra cosx, men var ikke sikker på regelen som ble anvendt. Nå vet jeg det. Takk for svar

PS: hvis noen, mot formodning, skulle gidde å lese mine tidligere innlegg fra 2013, under det nicket jeg bruker nå, så kan det være oppklarende å nevne at jeg siden 2013 har vært for opptatt med andre ting til å lese matte, inntil nylig, så er fortsatt noob på området.

Jeg ser jeg henvendte deg til min egen nettside, som siden 2013 har vokst enormt.

Jeg har ikke dekt U-pensum i nevneverdig grad, men 1T-kurset er en blanding av repetisjon av, og videre bygging på U-pensum, så det kunne vært en fin plass å starte. Hele kurset undervises her: http://udl.no/d/1t-matematikk

Det meste forklares gjennom eksempeloppgaver, men du burde naturligvis oppsøke bøker som har oppgaver du kan løse selv. Det vil ikke være dumt å kjøpe f. eks. Sinus 1T.

Etter 1T vil R1+R2 være logiske steg videre.

Takk for tips! Som nevnt tidligere, da jeg brukte navnet Anti, har jeg allerede lest R1 og R2. Er snart ferdig med forelesningene i MAT1100. Ved hjelp av UDL, Thue og video-opptakene av forelesningene på UiO har det vært overraskende enkelt å forstå matematikk, så langt. Men har nesten null mengdetrening, og er klar over at Lindstrøm skriver i Kalkulus at:

"... du må ikke tro at du forstår stoffet bare fordi du er i stand til å følge med på forelesningene. Det er oppgavene som er testen på forståelsen ... Én opplevelse har alle matematikkstudenter felles; å tro at de har forstått et kapittel, for så å oppdage at de ikke får til en eneste oppgave."

Men Arne Hole gjentar flere ganger i sine MAT1100-forelesninger at man ikke bør miste motet når man ikke får til alle oppgavene. Forståelsen kommer etterhvert, bare man ikke gir opp mengdetreninga.

For egen del er mitt første delmål kun å sjekke om jeg har IQ nok til å i alle fall kunne forstå matte-forelesningene som kreves for å ha en sjanse til å forstå kvantefysikk. Så skal snart begynne på lineær algebra, for å bare få et raskt overblikk over hvor vanskelig akkurat det er. Og deretter vende tilbake til massiv mengdetrening etter at jeg har fått et nogenlunde godt oversiktsbilde av hvor krevende matte generelt er. Kan velge denne litt uvanlige veien fordi jeg studerer matte som hobby, uten eksamenspress. Har derfor nok av tid.

Til slutt må jeg si mange takk til blant annet UDL. Det har gitt tilbake mye av matte-selvtilliten etter at en lærer knuste den på barneskolen. Med alle nett-ressursene som finnes i dag tror jeg de fleste kan lære matematikk, bare de er genuint interesserte.