Page 1 of 1
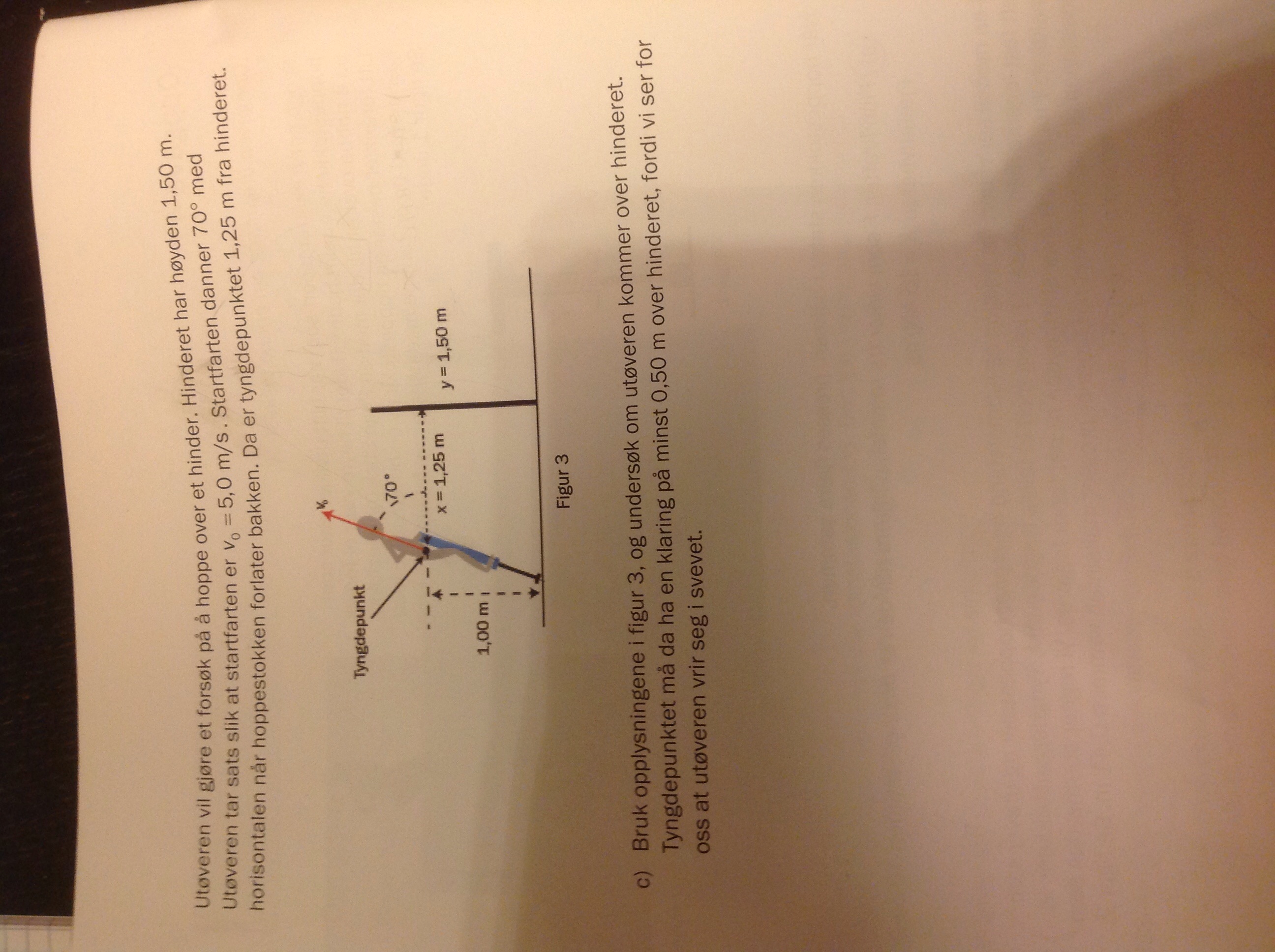
Vil utøveren komme over hinderet, fjær
Posted: 20/10-2016 20:09
by TRCD
Hei. Noen som har noe ide angående denne oppgaven?
- image.jpg (875.97 KiB) Viewed 1690 times
Re: Vil utøveren komme over hinderet, fjær
Posted: 20/10-2016 20:20
by Fysikkmann97
1. Finn uttrykk for strekningen i x-retning mhp. tiden. Den er som kjent konstant siden man ser vekk fra luftmotstand. Løs$ x(t_0) = 1,25 \,m$
2. Finn uttrykk for høyden i y-retning mhp. tiden. Sett inn i $y(t_0)$ og sjekk om $y(t_0) > 0 + klaring$ om du setter hinderet som nullpunkt, eller $y(t_0) > 1,5 + klaring$ om du setter bakken som nullpunkt. Er ulikheten sann, kommer han seg over.
$t_0$ er det tidspunktet der personen er ved hinderet.
Re: Vil utøveren komme over hinderet, fjær
Posted: 20/10-2016 20:21
by Dolandyret
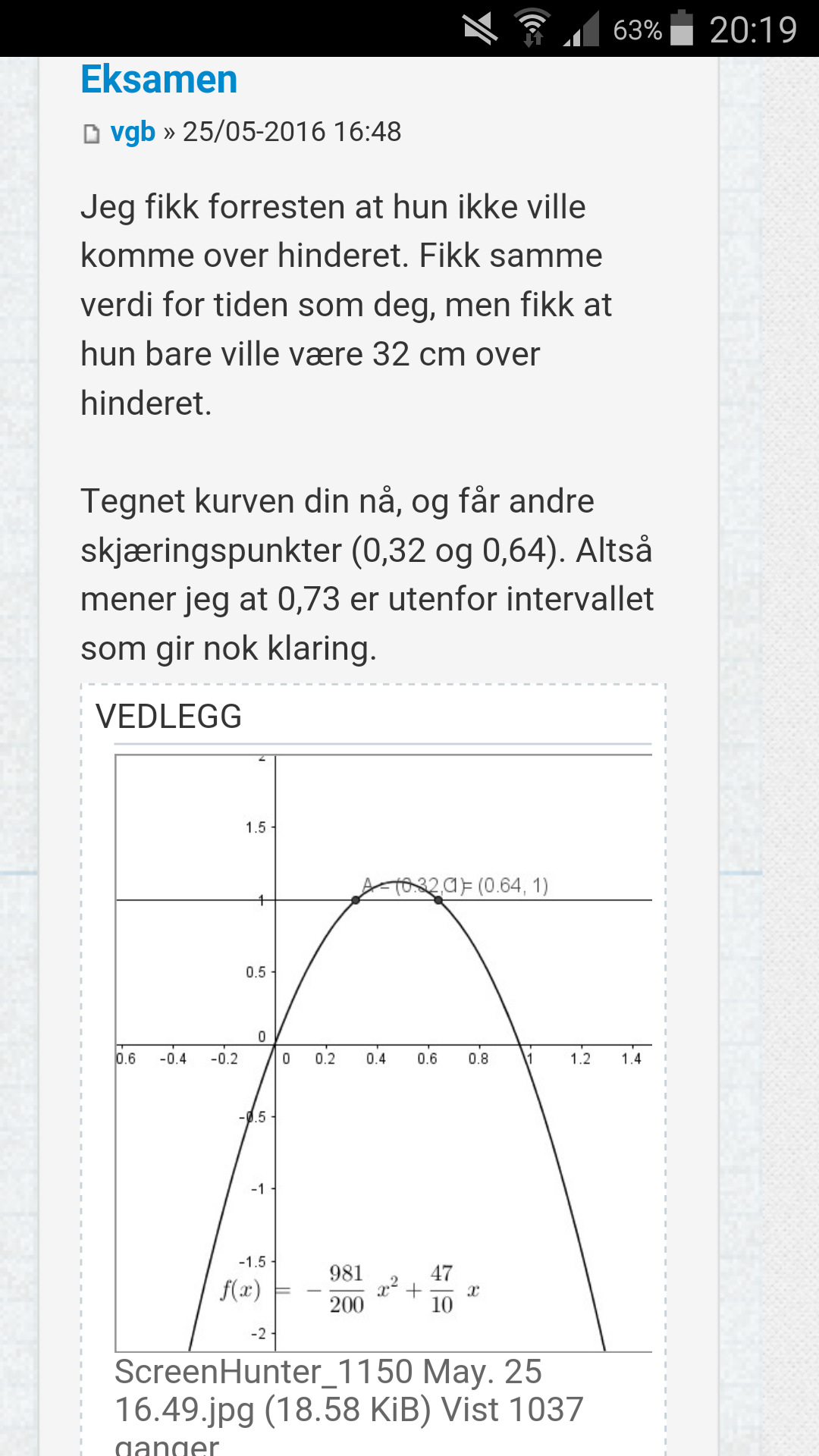
Fra en gammel tråd:
- Screenshot_2016-10-20-20-19-16.png (480.14 KiB) Viewed 1682 times
Re: Vil utøveren komme over hinderet, fjær
Posted: 20/10-2016 21:10
by TRCD
Fysikkmann97 wrote:1. Finn uttrykk for strekningen i x-retning mhp. tiden. Den er som kjent konstant siden man ser vekk fra luftmotstand. Løs$ x(t_0) = 1,25 \,m$
2. Finn uttrykk for høyden i y-retning mhp. tiden. Sett inn i $y(t_0)$ og sjekk om $y(t_0) > 0 + klaring$ om du setter hinderet som nullpunkt, eller $y(t_0) > 1,5 + klaring$ om du setter bakken som nullpunkt. Er ulikheten sann, kommer han seg over.
$t_0$ er det tidspunktet der personen er ved hinderet.
Skal jeg finne t0 utifra x(t0)=1,25 , for så å sette dette inn i y(t0) og sjekke om y(t0) blir større enn 1,50 + avklaring?
Re: Vil utøveren komme over hinderet, fjær
Posted: 20/10-2016 21:17
by Fysikkmann97
Ja, eventuelt kan du sette det opp som en parameterfremstilling, men iom. at jeg ikke kan noe om det så har jeg lagt frem min løsning. Setter du utgangspunktet til tyngdepunktet som nullpunkt, får du bare uttrykket $v_y(t) = 5 * sin(70^{\circ}) - gt$ som gir $y(t) = 5 * sin(70^{\circ}) * t - \frac 12gt^2$. Sett inn riktig t-verdi du kom frem til i punkt 1, så skal det bli noe under 1 m.