matematikk.net

Hei!
Lurte på om jeg kunne fått et løsningsforslag på oppgave 5 del 2 fra eksamen vår 2015.
Vet det ligger et løsningsforslag ute på nettet og har prøvd å se på det, men skjønner det virkelig ikke.

Hvis noen kunne vist meg alle mellomregninger som blir gjort og ikke bare noen få, hadde det vært supert

Du må være mere spesifik, det er rundt 10 ulike matematikk eksamener som blir laget hvert semester på videregående.

$A_{sirkel} = \pi (\frac 12 a)^2 = \frac 14 \pi a^2$

Areal av svart område:
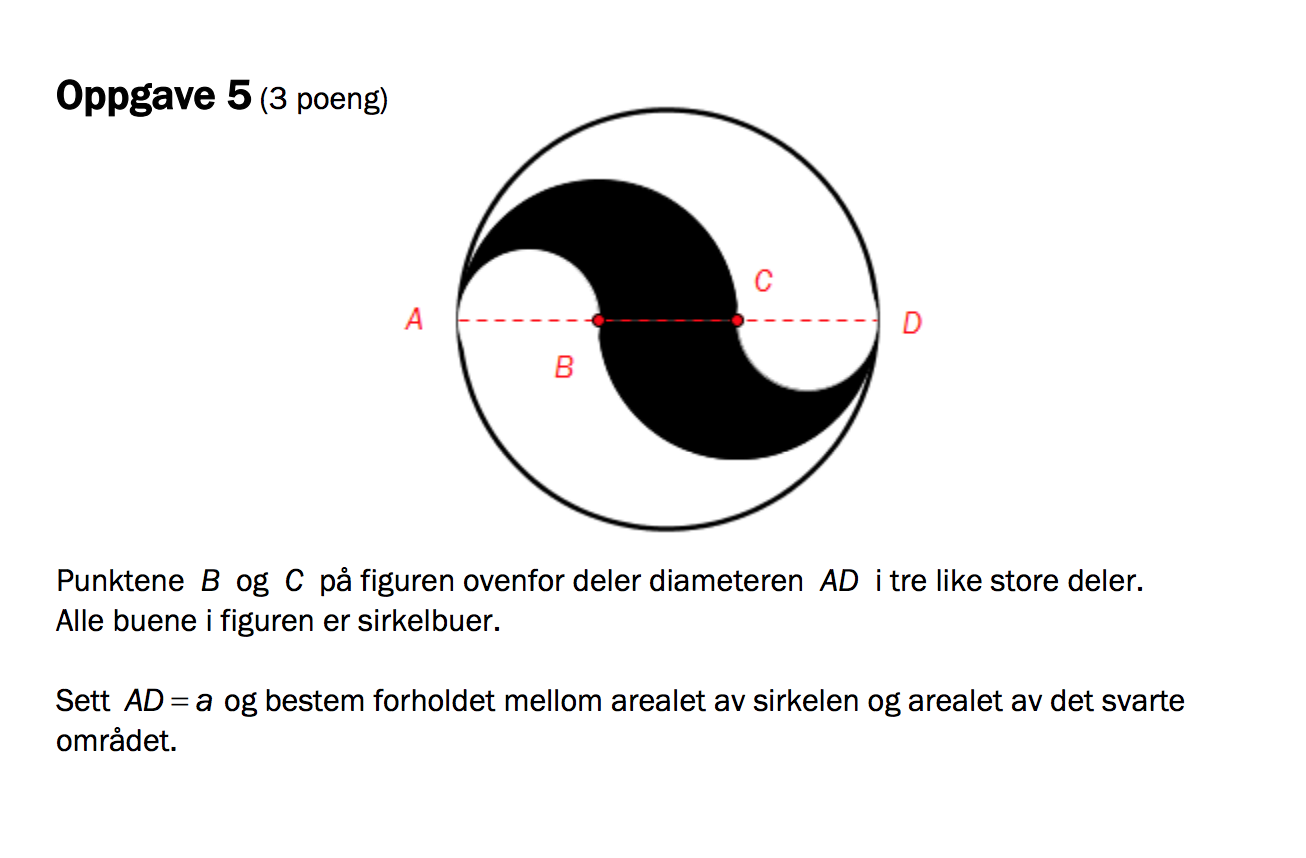
Om du flipper den nederste delen til andre siden, vil du se at man får en svart sirkel med diameter AC, som har en hvit sirkel med diameter AB inni seg. Arealet av det svarte området blir da $\pi(\frac 12 AC)^2 - \pi(\frac 12 AB)^2$ Får opplyst at diameteren består av tre like store deler, så siden $AD = \frac 33a$, så er $AC = \frac 23 a$ og $AB = \frac 13 a$ Setter dette inn i uttrykket:

$ A_{svart} = \pi(\frac 12 \frac 23 a)^2 - \pi(\frac 12 \frac 13 a)^2 = \pi(\frac 13 a)^2 - \pi(\frac 16 a)^2 = \pi \frac 19 a^2 - \pi \frac {1}{36} a^2 = \pi(\frac {4 - 1}{36}a^2 = \pi \frac {3}{36}a^2 = \pi \frac {1}{12}a^2$

Forhold: $\frac {A_{svart}}{A_{sirkel}} = \frac { \frac {1}{12}}{ \frac 14 } = \frac {4}{12} = \frac 13 = 33$ %

Oppgave 6 på abelkonkurransen i 1994 https://abelkonkurransen.no/problems/ab ... rob_nb.pdf

Tusen takk for svar!!! Nå forsto jeg den